#1 For each of the following problems, you are given a system of linear equations in matrix form, and you are given one or two points.
(i) Write the system in non-matrix form. Do not solve the system.
(ii) For each point given, determine whether or not it a solution to the system.
(iii) Check your answer in part (ii): Use Maple to plot the system and the given points, as demonstrated in class. If the point is a solution, make it green. If the point is not a solution, make it red.
(iv) Provide a printout of your plot, including all the blue output, as demonstrated in class. (Maple worksheet provided on course website.)

#2 For each of the following problems, you are given a system of linear equations in matrix form, and you are given one or two points.
(i) Write the system in non-matrix form. Do not solve the system
(ii) For each point given, determine whether or not it a solution to the system.
(iii) Check your answer in part (ii): Use Maple to plot the system and the given points, as demonstrated in class. If the point is a solution, make it green. If the point is not a solution, make it red.
(iv) Provide a printout of your plot, including all the blue output, as demonstrated in class. (Maple worksheet provided on course website.)

#3 You are given a system of linear equations in non-matrix form. Write the system in the matrix form,
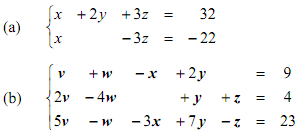
Av' = b'.
Do not solve the system.
#4 For each of the following, calculate whether or not the given point is a solution to the system indicated in #3 above. Show all steps.
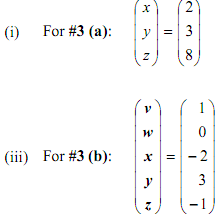
#5 Look at the assignments plus solutions from previous years for more practice.
Make sure you are comfortable converting back and forth between linear systems in matrix form and linear systems in non-matrix form. Make sure you understand what it means for a point to be a solution to a given system, both graphically and algebraically. If you have problems or questions, please let me know.