1. Samples of size n = 5 are collected from a process every half hour. After 50 samples have been collected, we calculate x'' = 20.0 and
s' = 1.5. Assume that both charts exhibit control and that the quality characteristic is normally distributed.
a) Estimate the process standard deviation.
b) Find the control limits on the x' and s charts.
c) If the process mean shifts to 22, what is the probability of concluding that the process is still in control?
2. Samples of n = 5 units are taken from a process every hour. The x'and R values for a particular quality characteristic are determined. After 25 samples have been collected, we calculate x'= 20 and R= 4.56.
a) What are the three-sigma control limits for x' and R?
b) Both charts exhibit control. Estimate the process standard deviation.
c) Assume that the process output is normally distributed. If the specifications are 19 ± 5, what are your conclusions regarding the process capability?
d) If the process mean shifts to 24, what is the probability of not detecting this shift on the first subsequent sample?
3. Thirty samples each of size 7 have been collected to establish control over a process. The following data were collected:
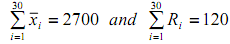
a) Calculate trial control limits for the two charts.
b) On the assumption that the R chart is in control, estimate the process standard deviation.
c) Suppose an s chart were desired what would be the appropriate control limits and center line?
4) Control charts for x' and R are in use with the following parameters. The sample size is n = 9. Both charts exhibit control. The quality characteristic is normally distributed.
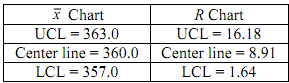
a) What is the α-risk associated with the x' chart?
b) Specifications on this quality characteristic are 358 ± 6. What are your conclusions regarding the ability of the process to produce items within specifications?
c) Suppose the mean shifts to 357. What is the probability that the shift will not be detected on the first sample following the shift?
d) What would be the appropriate control limits for the x' chart if the type I error probability were to be 0.01?