Calculate the variance-covariance matrix of the ols

Question

Question 1

A regression equation with three regressors X₁,X₂ and X₂, is obtained be regressing (yi - y) on (xi1 - x₁), (x2 _-52) and (2,3 - 23) for t = 1 V where g, 2₁, 2₂ and 23 are the sample averages of the regressand y and the three regressors. The observed values of X'X, where

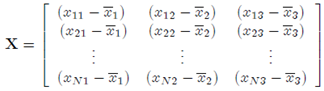
is the (N x 3) matrix of observed deviations from the average, is

Suppose that you estimate the regression model

y = X₁β, + X₂β₂ + X₂β₃ + e

where e satisfies the classical assumptions and has sample variance s² = 32. Calculate the variance-covariance matrix of the OLS estimator of β₁.β2 and β₃ and verify that:

1. The variance of bi is directly proportional to the reciprocal of the observed variance of X_i.

2. The variance of each 62 and 63 is bigger than that of b_i even though the observed variance of X2 and X3 is the same as that of Xi. Why is this the case?

3. The covariance between b₂ and b₃ is positive. Provide a heuristic explanation of this feature.

Attachment:- EM201448JOH328ASTAT_Question.docx