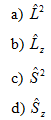Calculate the value of x2 for the first excited state of a

Question

1.  Evaluate the following integrals:

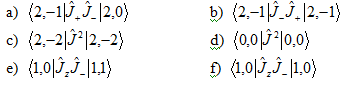
2. Calculate the value of (x²) for the first excited state of a harmonic oscillator (given above).

3. The radial wave equation is written as:

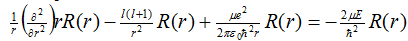
where R(r) is the radial wavefunction and bound state energies are always negative.  Show that the wavefunctions must decay exponentially (as a function of exp(-r)) as r à ∞.  Note that for the solution to be an acceptable wavefunction it must decay to zero at infinity.  This exponential decay is implicated in several chemical reaction types.

 

4. For an electron in the quantum state|l,m_l,s,m_s) = |1,-1,½,-½) find the eigenvalue of the following operators: