Calculate the natural frequency and sketch the tr mode

Question

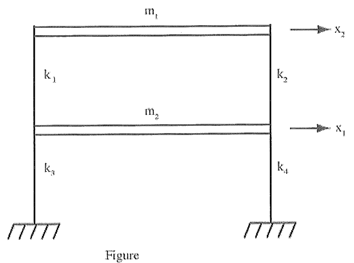
1. SHEAR BUILDINGS

For the shear building shown, determine the natural frequencies (RAD/SEC) and the modal matrix. Also, sketch the deflected buildings in their normal modes using the top floor as the reference floor (set its displacement = unity). Finally, demonstrate orthogonality between the modes with example calculation.

• All k factors (stiff nesses) = 15,000 LB/IN
• m₁ = 50 LB-SEC²/IN
• m₂ = 150 LB-SEC²/IN

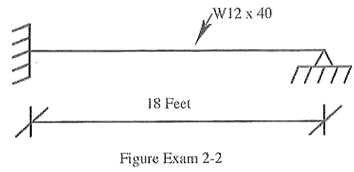
2. BEAMS WITH DISTRIBUTED PROPERTIES

Calculate the 4^th natural frequency and sketch the tr mode shape (reasonably to scale) for the beam shown. E = 29x10³ KSI.

3. BEAMS WITH DISTRIBUTED PROPERTIES - FORCED VIBRATION

Consider the beam shown. P_o is a concentrated load applied suddenly (both loads simultaneously) where shown.

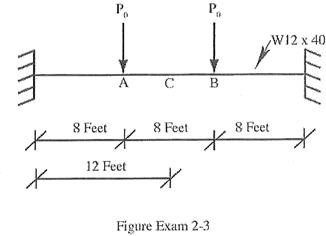
A. Discuss or calculate the relative contribution to the total deflection at point A of the 2^nd mode of vibration compared to the la mode.

B. What is the ratio of the contribution to the total deflection at point C of the 3^rd mode relative to the 1" mode?

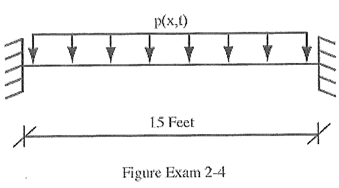
4. DYNAMIC ANALYSIS OF BEAMS WITH DISTRIBUTED PROPERTIES

For the beam shown, and considering only the 1^st mode, determine the maximum deflection 7.5 FT from the left support.

• El = 30x10⁸ LB-IN² (constant)

• m'= 1 LB-SEC²/IN per inch of beam span

• Uniform impulse force p(x,t) = (2000)sin(400t) LB acting during a time interval equal to half of the period of the sinusoidal load function (that is, t_d = Π/400 SEC).