Assignment 1:
QUESTION 1:
Your firm is considering building a $600 million plant to manufacture a product in a sector outside its main business. You expect operating profits (EBITDA) of $145 million per year for the next 10 years. The plant will be fully depreciated on a straight-line basis over 10 years. After 10 years, you expect to be able to sell the plant as scrap metal for $300 million. The project requires $50 million in working capital at the start, which will be recovered in year 10 when the project shuts down. The corporate tax rate is 35%. All cash flows occur at the end of the year.
a. Calculate the free cash flows that the new plant will generate.
b. Assume the risk-free rate is 5%, the market risk premium is 6%, and the asset beta for your industry is 1.20. Would you invest in the plant? Why? [Hint: assume for this part that the plant is financed with equity only]
c. Consider the following information for publicly traded companies operating in the sector of the new plant.
Company Equity Beta Debt Beta DIE
X 1.85 0.2 0.25
Y 1.8 0 0.05
Why and how does this additional information affect your investment decision? Explain. [Hint: assume for this part that the plant is financed with equity only]
d. You consider financing $50 million of the cost of the plant using privately placed debt at 9%. The principal will be repaid in equal amounts over the next 4 years (the outstanding debt will be $37.5 million at the end of the first year, $25 million at the end of the second, and so on). This amount is incremental new debt associated specifically with this project and will not alter other aspects of the firm's capital structure. Calculate the value of the project with financing. How does your investment decision change? Explain.
e. The firm's investment committee meets to review your decision. A member of the committee goes over your numbers and argues that you have not included the value of diversification that the new plant will bring to existing investors. Based on his remark, how do you adjust your investment decision? Explain.
QUESTION 2:
Two competing entrepreneurs set up toy stores across the street from each other. Both stores are identical in their required investment, expected cash flows, and duration. The required investment is 40. The cash flows (of each store) are 120 with probability 1/3 and 60 with probability 2/3. The stores live for only one period and there is no discounting. The only difference between the stores is that the first one, Debts'R'Us, raises the 40 required for investment issuing debt, and the second store, FAO Equity, raises it issuing equity. [Hint: assume throughout this question that the entrepreneurs of each store only care about their own payoffs]
a. What is the promised repayment to debtholders by Debts'R'Us? What fraction of firm's equity does FAO Equity have to promise to raise the required funds? Are the values of the entrepreneur's equity of the two firms equal? Why or why not? Explain.
b. Suppose that a few months after the entrepreneurs raise the funding and make the investment as in part a., a large discount toy store opens one block down the street. Competition drops the cash flows of Debts'R'Us and FAO Equity by 30 in both scenarios. That is, the cash flows (of each store) are 90 if the stores do well, and 30 if they do poorly. Are the values of the entrepreneur's equity of the two firms equal? Why or why not? Explain.
c. Suppose that the stores can be restructured to respond to the competitive threat of the discount store. Restructuring each store costs R. Restructuring increases the probability that the store is a success by 1/3, from 1/3 to 2/3 (restructuring does not affect the cash flows, which are still 90 if the store succeeds and 30 if it does not). Suppose that the toy stores can pay for the restructuring cost using internally generated cash. For what values of R does restructuring increase the total value of the toy stores? For what values of R will Debts'R'Us restructure? For what values of R will FAO Equity restructure? Are the three ranges of R the same? Discuss why or why not.
d. Suppose that R is low enough that the entrepreneurs would want to restructure if they had the internal funding. However, suppose they do not have the internal funding and instead, the firms must raise new junior debt to fund the restructuring cost. For what values of R will the restructuring occur in each firm? (Hint: new junior debt has priority over equity, but not over existing debt).
e. Without doing any calculations: consider how your answer changes if the firms raise equity to pay for the restructuring cost instead of debt. In particular, how would the ranges of R for each firm differ from those in parts c. and d.?
QUESTION 3:
SoftGames, a small IOS software firm, designed its first App, AngryDogs, and funded the investment fully with equity of the entrepreneur. The App may be either a potential blockbuster or mediocre. If it is a blockbuster, the cash flows are 100 with probability 1/2 and 40 with probability %. If it is mediocre, the cash flows are 60 with probability 1/2 and 40 with probability 1/2. Management knows whether the App is mediocre or a blockbuster. However, outside investors do not, and assign equal probability to each scenario.
a. What is the market value of the equity of SoftGames? What is the actual value if the App is a blockbuster? What is the value if the App is mediocre? Assume throughout that there is no discounting and Apps last for one period only.
The entrepreneur has an idea for a second App, AngryCats, which requires an investment of 10 and will produce a cash flow of 40 for sure. The entrepreneur does not have any money left, so she has to raise outside funds to invest in the new App.
b. Suppose SoftGames decides to fund the second App with outside equity. Suppose that investors are naïve and do not infer any information from the actions of the firm. If management knows that AngryDogs is a blockbuster, what is the true value of the entrepreneur's equity after raising the new funding? Does the entrepreneur keep the full NPV of the new project? Why or why not? How does your answer change if SoftGames knows the first App is mediocre?
c. Suppose SoftGames issues debt to fund the second App (and investors are still naïve). What is the true value of the equity after raising the new debt if the first App is a blockbuster? What is the true value of the equity if the first App is mediocre? Is your answer different from part b.? Discuss why or why not.
d. Suppose now investors are rational (not naïve). Given your answers to b. and c., what will investors infer about the prospects of the first App if SoftGames issues equity? If it issues debt? Discuss under which circumstances it makes sense for SoftGames to issue equity.
e. Suppose that the new App is risky: cash flows may be 0 or 80 with equal chance. Without doing any calculations, discuss whether or not your answer to d. changes in this case.
4. This question is about bonds, forwards, and immunization
Consider two bonds. Bond 1 is a three-year zero with face value £100 and maturity in June 2017, and bond 2 is a two-year 10% annual-coupon bond with face value £100 and maturity in June 2016. Current prices of bonds 1 and 2 in June 2014 are £72 and £103, respectively. Moreover, there are two annuities, which are traded at equal prices. The first one is a three-year annuity that pays £10 and matures in June 2017, and the second pays £14 and matures in June 2016.
a) What are the discount factors di, d2, d3 in the economy?
b) What are the prices of the annuities?
c) Determine the forward rates 2f1, and 1f2 in this economy.
d) Consider a perpetuity with growth that makes annual payments starting in year 4. The first payment is £10, and then the payment grows at a rate of 1% forever. Consider a forward contract that delivers this perpetuity in year 3. What is the forward price at date 0 if the term structure is flat at r=2%? Suppose, in year 1 the term structure shifts to 1.8% and remains flat. What is the value of the forward in year 1? [Hint: do not confuse forward price with forward value.]
e) An insurance company needs to pay £1 million in both years 3 and 4 from now. The term structure is flat at r=2%. What is the present value of the company's liabilities?
f) What is the Macaulay duration and modified duration of the insurance company's liabilities?
g) Suppose, the insurance company in part e) decides to immunize its liabilities. Its current assets are in cash, and the net worth is zero. The firm decides to invest half of its cash in 2-year zeros and the other half in T-year zeros, both with face value £100. What should be the maturity T for this immunization strategy to work?
5. This question is about portfolio choices and the CAPM
a) You are thinking about investing in a portfolio of two stocks: Glaxo and BP. These stocks are expected to perform differently depending on the economic environment. Assume the good economic outcome has a probability of 0.75 and the bad economic outcome has a probability of 0.25. The payoffs of Glaxo and BP are described in the table below. Calculate the expected returns and standard deviations of Glaxo and BP, and their correlation coefficient.
Bad Economy Good Economy
Glaxo -12% 12%
BP -16% 20%
b) Calculate the expected return and standard deviation of a portfolio that invests £10,000 in Glaxo and £10,000 in BP.
c) How would your answer to part b) change if you borrowed £10,000 at the risk-free rate (4%) to finance your investment (i.e., your net wealth was £10,000).
d) Suppose a friend of yours tells you that he has invested £20,000 in a portfolio of Glaxo and BP stock, but does not tell you his portfolio weights. He does tell you, however, that he had to borrow £4,000 at the risk-free rate (which is 4%) and that the expected return on his portfolio is 9%. How much money did your friend invest in each stock?
e) The CAPM says that stocks with higher betas are riskier, and should therefore have higher average returns. How is the "beta" of a stock defined, mathematically? How would you explain intuitively, to someone with little training in finance, what beta captures?
f) Explain why the change in portfolio variance when you add a small amount of a stock to your portfolio is largely determined by the stock's covariance with your portfolio.
g) Assume the CAPM holds and consider two firms X and Y such that
var(r) cov(r, rMarket) E(r)
stock X 3 2 8%
stock Y 9 4
Assume that the risk free rate is 5%, what is the expected return of stock Y?
6. This question is about market efficiency and behavioral finance
a) What is the definition of "market efficiency"? Explain the distinctions among the three forms of market efficiency.
b) Briefly describe two pieces of evidence that suggest that markets are semi-strong-form efficient.
c) We talked about two building blocks for behavioral finance, which study situations where the Efficient Market Hypothesis may break down. Describe these two building blocks.
d) In class, we saw that, when a company announces surprisingly good earnings news, its stock jumps up immediately, but then keeps rising in the weeks thereafter. A recent study has found that this effect — i.e. the subsequent upward drift — is particularly strong for firms which announce earnings on the same day as many other firms. In other words, the greater the number of firms announcing earnings on a particular day, the stronger the subsequent drift for those firms, after their earnings announcements. What is the most plausible interpretation of this evidence?
e) Some recent studies on the post earnings announcement drift find that the return predictability is concentrated around subsequent earnings announcement dates. For example, a firm that announced unexpectedly high quarterly earnings in April 2013 is likely to have high stock returns around the subsequent quarterly announcements (e.g., July and October 2013). What is a plausible interpretation of this evidence?
f) Briefly describe the twin-stock (-share) puzzle. We have discussed a number of possible explanations for this puzzle. List two of them.
g) Stock indices, such as the S&P 500, are typically "value-weighted." In other words, the weight a firm is assigned in the index depends on its market capitalization. If firm A has twice the market capitalization of firm B, then firm A is assigned twice the weight of firm B in the index.
Recently, a new product known as a "fundamentals index" has emerged on the financial scene. With fundamentals indices, the weight a firm is assigned in the index depends on some measure of fundamentals, such as sales. So, if firm A has twice the sales of firm B, then firm A is assigned twice the weight of firm B in the index.
Advocates of fundamentals indices argue that, if markets are inefficient, these indices will earn higher average returns than traditional value-weighted indices. Can you see the argument for why this would be true?
Assignment 2:
Question 1:
In early 2015, British Home Artifacts (BHA), a manufacturer of household products, was considering expanding into the prescription drug business. BHA is considering Polonium United (PU) as a target for an acquisition. PU is a publicly traded anti-depressant manufacturer, with a 2014 year-end equity market capitalization of £4,000 million. BHA's CEO considers that PU is currently mismanaged, but that under his efficient management team it would be reasonable to expect PU's EBIT, net working capital, and net fixed assets to grow at a constant rate of 8% for the foreseeable future. The following table shows selected financial statement information for PU by year-end 2014. (Hint: this is a valuation question.)
From end of 2014 Financial
Statements
(Millions of £)
From Income Statement
EBIT 500
From balance sheet
Cash and marketable securities (*) 1000
Inventory and Acc. Receivable 2000
Accounts Payable 1500
Net Fixed Assets 1000
Total Debt (Interest bearing) 3000
Other Information
Corporate Tax Rate 25%
*Assume that cash and marketable securities are not necessary for the operations of the firm.
a) Suppose PU were acquired today, that BHA's CEO growth projection is correct, and that PU's opportunity cost of capital is 12%. What is the value of the unlevered operating assets of PU?
b) Suppose that PU's net debt will also grow at a constant 8% for the foreseeable future. Assuming that the interest rate on the (net) debt is 5% and that the opportunity cost of the debt tax shield is equal to the opportunity cost of capital: what is the value of the debt tax shield?
c) Maintain the assumptions in parts a) and b). Using the APV valuation method, what is the maximum amount BHA should be willing to pay for PU's equity today?
d) Suppose the debt to equity ratio going forward is the one implied by your answer to part c). Recalculate the value of equity using the WACC valuation method. Is the answer the same as in part c)? Explain why or why not. [Hint: calculate the cost of equity using the formula r, = r, + DIE - rd)]
e) Suppose PU's equity beta, obtained using PU's stock market returns during the last year, is 3. How would your answer to part a) change in that case? Explain. (Assume that the beta of debt is zero, the market risk premium is 6%, and the risk free rate is 2%)
f) BHA's CEO made a strong case for the acquisition of PU on the basis of two arguments. First, BHA had substantial unused cash and debt capacity, which provides a low cost source of funds for underwriting the acquisition. Second, the lack of overlap between BHA and PU operations would provide BHA shareholders with significant diversification that would reduce the risk of holding BHA stock. Discuss these two motivations in light of the concepts discussed in the lectures.
Question 2:
Tasco is a well-established company that sells apples, the value of the assets in place is 100 and it has no debt. The CEO of Tasco is considering entering the pear business, which would represent a net loss for Tasco of 20, but, generates private benefits to the CEO of 1.5. The CEO owns 5% of the company. The discount rate is 0 and there are no taxes.
a) Will the CEO invest in the pear business? Would the CEO's incentives to invest in the pear business change if he owned 50% of the equity? Explain.
b) Suppose the firm does a recapitalization: it issues debt with face value of 80 and uses the proceeds to buy back shares (assume that the CEO does not tender any shares in the recapitalization and that the CEO and investors believe the debt is risk-free). Will the CEO invest in the pear business now? Explain.
c) What is the minimum value of debt to be issued in the recapitalization such that the CEO will not invest in the pear business?
Assume that after Tasco undertakes the recapitalization described in part b. (i.e., the company issues debt with face value of 80 and buys back shares), its main competitor Waitviolet, launches an aggressive competitive attack that reduces the value of Tasco's assets to 70. The CEO devices two different strategies to counter Waitviolet's attack. The first is a marketing campaign that costs 20 and generates additional cash flows with a value of 25 for sure. The second is a risky apple production technology that also costs 20, and generates additional cash flows valued in 50 with probability 50%, and no additional cash flows with probability 50%. The safe and risky strategies are mutually exclusive: Tasco can take either the safe strategy or the risky one, but not both.
d) Suppose that Tasco has enough internal cash to fund the cost of 20. Which strategy has a higher NPV? Which strategy will the CEO prefer? Explain.
e) Suppose Tasco does not have internal cash to fund the investment. Will Tasco be able to raise 20 from outside investors by issuing new junior debt? And by issuing new equity? Explain.
f) Use your answers to parts b., d., and e. to discuss how capital structure may affect firm value and the advantages and disadvantages of using debt.
Question 3:
An entrepreneur has designed a new consumer electronics gadget that is ready for mass production. Setting up the manufacturing facilities has a cost of 500. Potential investors do not know whether the gadget will be a hit or a flop. Investors believe that with an 80% chance the gadget will be a flop and generate cash flows with a present value of 250. With 20% chance the gadget will be a hit and generate cash flows with a present value of 2000.
a) If the entrepreneur issues equity: what fraction of the equity will be required by investors? If the entrepreneur issues debt: what promised repayment amount will be required by investors (promised repayment = present value of payment to debt holders if the gadget is a hit)?
b) [Hint: assume for this question that investors are naïve and do not infer any information from the type of security issued] Suppose the entrepreneur knows the gadget will be a hit. What is the NPV of the investment? What is the value of the entrepreneur's equity stake if he issues equity as in part a)? What is the value of the entrepreneur's equity stake if he issues debt as in part a)?
c) Do the assumptions of the Miller and Modigliani irrelevance proposition hold in part b)? Explain why or why not.
d) Suppose the entrepreneur in part b) could convince investors that if the gadget were a flop the present value of the cash flows would be no less than 500. Can the entrepreneur raise debt and keep the full value created by the project? Explain.
e) Suppose investors are smart and try to infer whether the project is a hit or a flop from the type of security the entrepreneur issues. Will an entrepreneur that knows the gadget is a flop ever attempt to issue equity? Will he attempt to raise debt? Discuss, without doing any calculations, whether a smart investor can ever believe that entrepreneurs with a project that is a flop never attempt to raise financing (Hint: what will be the best course of action for an entrepreneur with a project that is a flop if investors have those beliefs?).
f) Suppose investors are smart and that the entrepreneur can take an action that makes it personally very costly to him to pay less than the promised value on the debt (stake his reputation as a businessman, pledge as collateral a family heirloom with a large sentimental value). Will the entrepreneur that knows the project is a flop want to take that action? Will the entrepreneur that knows the project is a hit? Will the entrepreneur that knows the project is a hit be able to keep the full NPV of the project when the costly action is available to all entrepreneurs? Explain.
4. This question is about option valuation
a) FM429's stock price is £110 and in each 3 month period will either increase by 25% or fall by 20%. A 6-month European call on FM429 stock has an exercise price of £90. The interest rate is 3% every 3 months. What is the value of the European call option on FM429?
b) Suppose that at the end of month three, the FM429 stock price is £88. How at that point would you replicate an investment in the stock by a combination of the European call option and risk-free asset?
c) What is the value of a 6-month European put option on FM429 with an exercise price of £90?
d) Verify that put-call parity holds.
e) What is the value of a 6-month American put on FM429 stock with an exercise price of £110? Would investors ever want to exercise this American put early?
f) Now suppose that the stock, FM429, pays a dividend of £12.50 every three months. What is the value of a 6-month American call on FM429 with an exercise price of £90? Would you ever want to exercise this American call early?
5. This question is about forward, futures, and swap contracts
a) Consider a two-year forward contract delivering a two-year coupon bond with a face value of £100 and coupon rate of 20%. The forward price F will be paid in year 2 while the bond payments occur in years 3 and 4. The term structure is given by rti=3%. ro,2=4%, r3,3=4.5%, r0,4=5%. Find the forward price F.
b) Suppose, one year later the term structure becomes rQ1=2%, ro.2=3%, r0.3=3.5%, ro.4=4%. What is the new value of the contract with forward price as in part a)?
c) Consider a 4-year interest rate swap that each year exchanges fixed payments at rate k to the cash flows of a floating rate note with spot annual interest rate rt_i.t. The term structure is given by 1'0,1=3%, r02=4%, 1.0,3=4.5%, r0,4=5%. Find the fixed rate k.
d) Suppose, one year later the term structure becomes ro1=2%, r0.2=3%, 1'0,3=3.5%, rm=4%. The notional amount is £100. What is the value of the interest rate swap in part c) at t=1 (after the first cash flow is exchanged) to the parties of this contract?
e) The current exchange rate is $1.65 for £1. The short-term annual interest rate in UK is 2%. Suppose, one-year futures exchange rate is $1.6 for £1. What should be the interest rate in the US to avoid arbitrage opportunities?
f) Assume that the 1-year risk-free interest rate is 6%. There is a temporary, unexpected glut of wheat on world markets due to an unusually large harvest. Storage costs are £10 per ton per annum (assume costs are paid at the end of the year). The spot price of wheat is £600 per ton. What is the approximate futures price of wheat for delivery in one years time?
g) List three key distinctions between forward contracts and futures contracts. What is the additional source of risk faced by investors in forward contracts?
6. This question is about market efficiency
a) Briefly describe two pieces of evidence that violate the weak form of market efficiency.
b) Carhart (1997) finds that, after fees, actively-managed mutual funds do not outperform the stock market on average. Is this evidence consistent with market efficiency? What is the main benefit of investing in mutual funds? Also discuss why it is not surprising that actively-managed mutual funds are unable to outperform the market, even if these active managers are skilled.
c) Sometimes on earnings announcement days, firms with positive earnings growth (relative to the prior year) suffer large stock price drops, whereas firms with negative earnings growth experience large stock price appreciations. Is this a violation of market efficiency? Why?
d) What is noise trader risk? Explain the mechanism through which noise trader risk can become an important deterrent to arbitrage activity.
e) An important test of the efficient market hypothesis is whether some investors can persistently outperform the market. Suppose that in any given year, there is a 50% probability that mutual fund X will outperform the market simply by chance. If X is the only mutual fund, calculate the probability that it will beat the market for 10 consecutive years due to chance
f) Now, recognize that there are over 10,000 mutual funds in the United States. What is the probability that, by chance, there is at least 1 (out of 10,000 funds) that outperforms the market for 10 consecutive years?
Assignment 3:
Question 1:
a. Mutual fund Q has an average annual return of 19%, with a standard deviation of 25% and a beta of 2. Further assume that the annual return to the market portfolio is 9% with a standard deviation of 10%. The risk free rate in the economy is 3%. What is the Sharpe ratio, M2, Jensen's alpha, Iltynor ratio, and information ratio (IR) of this fund Q?
b. Derive the mathematical relationship between the Treynor measure and Jensen's alpha. Do these two measures always give the same ranking since both consider the tradeoff between return and the (CAPM) market risk?
c. In the lleynor-Black model, each investor maximizes the Sharpe ratio of his portfolio that comprises an active portfolio (that he believes to have a non-zero alpha) and the market portfolio. Suppose that you can invest in fund Q described in (a) and another active fund P where its αp = 3% and its idiosyncratic risk σep = 9%. That is, you need to form a final active portfolio using fund Q and fund P before combining this final active portfolio with the market portfolio. In this final active portfolio, what are the relative weights you should invest in fund Q and fund P? Calculate the information ratio (IR) of this final active portfolio. Describe intuitively why IR is useful for hedge fund managers.
d. Market timing refers to investors' ability to forecast market returns. Describe one empirical test of an investor's market timing ability. In particular, a) write down the regression equation of the test; b) explain how to interpret the regression coefficients.
Question 2:
You are the portfolio manager for an equity fund whose base currency is the Pound Sterling (GBP). During the month of February 2013, a portion of your portfolio is invested in stock issued by company X. This stock is denominated in Euros (EUR) and traded in the Eurozone. The following data applies to this question:
• GBP-EUR exchange rate on 31 January 2013: 1.1680
• GBP-EUR exchange rate on 28 February 2013: 1.1611
• Annualized one-month GBP risk-free interest rate on January 31st, 2013: 0.4925%
• Annualized one-month EUR risk-free interest rate on January 31st, 2013: 0.0557%
• EUR monthly return on company X stock for February 2013: 5.36%
Note: all exchange rates above are quoted in units of EUR per 1 GBP. Please express any exchange rates in your answer using the same convention.
Your task is to compute the returns on your investment, decompose it into equity ana currency effects, and correctly interpret your calculations and answers. You can assume that there are no transaction costs, bid-ask spreads are zero, borrowing and lending risk-free rates are identical, there is no counterparty risk and capital flows between the United Kingdom and the Eurozone are free.
a. What expression would you use to compute the currency-unhedged GBP-denominated return on your investment in company X stock during February 2013? Justify your answer, and compute this return.
b. How would you compute the appreciation/depreciation of the EUR relatively to GBP? What was this appreciation/depreciation during February 2013?
c. One of your clients, whose base currency is the GBP, tells you that by subtracting the currency appreciation/depreciation (calculated in part (b)) from the unhedged equity return (calculated in part (a)), he would find out how much returns he would have earned in company X stock if he had hedged his currency exposure. How would you respond to him? (No calculations are needed for this item.)
d. Assuming covered interest parity holds, what is the one-month forward GBP-EUR exchange rate on 31 January 2013? Describe the market mechanisms that ensure no deviations from this value.
e. Suppose that on 31 January 2013 you do not expect any movement in GBP-EUR spot exchange rate for the next month. How would you implement a carry trade between GBP and EUR to take advantage of your view?
f. Compute the currency return for the EUR in GBP terms during February 2013. Justify your methodology.
g. Upon seeing your calculation of currency returns from f, the client states that he would like to compute his currency-hedged returns in company X stock using the formula
RH = (1 + RU/1 + RC) - 1
where RH is the hedged equity return, Ru is the unhedged equity return (from part (a))and RC is the currency return (from part (f)). What result does this yield for the hedged equity return? What are the advantages and disadvantages of using this methodology?
h. Compute the hedge impact (as defined in the class notes) that applies to your investment in company X stock. The hedge is accomplished using the forward market to offset your initial currency exposure and does not need to be addressed during the month. How would you use this hedge impact to compute hedged equity return in company X stock as an alternative to part (g)? What are the advantages/disadvantages of choosing this approach?
Question 3:
In one of the homework problems, you have collected data on market capitalisation of five industries (US$ billion) at the end of December 2012:
Consumer Manufacturing Technology Healthcare Other
2866.47 3712.95 3911.41 1546.73 3654.89
In this question, your task is to form an optimal portfolio with these five industry sector indices using the Black-Litterman (BL) model.
a. First, compute market portfolio weights for each industry sector. Second, you have also collected data on the five value-weighted sector indices. Denote the variance-covariance matrix of five industry index returns (annualised) as E. Denote the risk-aversion parameter of a representative agent as A, which is set to be 1. Carefully explain how you derive the market expectation of these five sector returns theoretically, which is denoted by H. Suppose the new estimate of A is 2, how would you change your derivation of the market expectation of these five sector returns? If you agree with the market expectation of these five sector returns, how would you form the optimal portfolio weights?
b. Now you have doubt about the market expectation of these five sector returns. Specifically, you have the following prior belief on the true expected return denoted as A:
μ = Π + ε
where ε is distributed normally with mean 0 and variance-covariance matrix Σ. Suppose r = 0.05, how would your optimal portfolio weights change? Suppose τ = 0.5, how would your answer change? What does parameter τ measure?
c. Besides the prior belief specified above, you have also formed the following three views after researching these five sectors. Specifically, 1) you believe that the technology sector is over-weighted and this sector expected return will be 2% per annum, and we denote this as view 1; 2) you believe that the healthcare sector will outperform the manufacturing sector by 5%, and we denote this as view 2; 3) you also believe that the consumer sector will outperform the market value-weighted average of healthcare and technology by 2%, and we denote this as view 3. Specify these views in terms of P and Q.
d. You also have doubts about the validity of your own views.
Pμ = Q + εv
where εv is distributed normally with mean 0 and variance-covariance matrix 0 where
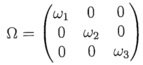
What is the role of Ω (that is, wi where i = 1, 2, 3 as in view 1, 2, 3) in the BL model?
e. Carefully explain how to combine your own private views with the prior to obtain posterior expected return (denoted by A) and posterior variance-covariance matrix E theoretically (that is, you only need to write down mathematical expressions).
f. Suppose that all agents in the economy share the same risk-aversion which is 1, how do you use μ‾ and Σ‾ to form optimal BL portfolio? In this optimal BL portfolio, what is your portfolio weight on the 'other' sector if τ = 0.05? Suppose w3 associated with view 3 is infinitely large, what is your portfolio weight on the consumer sector? Discuss.
g. Suppose that, in addition to the views in part (e), you have obtained the expected return estimates (A) from a reputable stock analyst on these five sectors and
μˆ = μ + εs
where the noise term e is distributed normally with mean 0 and variance-variance matrix SE. How would your answer to part (e) change?
Question 4:
a. Describe in detail time-series and cross-sectional tests of the CAPM.
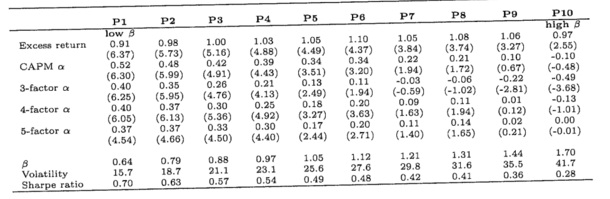
b. A recent paper by Frazzini and Pedersen (2013) presents monthly returns from portfolios of U.S. stocks. At the end of each month stocks are ranked in ascending order on the basis of their estimated beta. The portfolios are equally weighted and rebalanced every month. The sample includes all U.S. stocks between 1926 and 2012. The table below reports returns in excess of the risk-free rate, CAPM alphas, 3-factor alphas (Fama¬ftench), 4-factor alphas (Carhart) and 5-factor alphas (Pastor-Stambaugh). Returns and alphas are in monthly percent (t-statistics are shown in parentheses). Beta is the average pre-estimated beta at portfolio formation. Volatilities and Sharpe ratios are annualized. Interpret the results shown in the table. How do they relate to the empirical evidence on the CAPM?
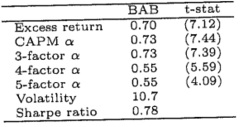
c. The same paper then constructs a new factor, called BAB. To construct BAB, all stocks are assigned to one of two portfolios: low beta and high beta. Stocks are weighted by their ranked betas (lower beta securities have larger weight in the low-beta portfolio and higher beta securities have larger weights in the high-beta portfolio). The BAB factor is a self-financing portfolio that is long the low-beta portfolio and short the high-beta portfolio. The portfolios are rebalanced every month. Both portfolios are resealed to have a beta of 1 at portfolio formation. Below are the monthly returns to the BAB factor (t-statistics are shown in parentheses). Interpret the findings from this table. How could an investor use these results?
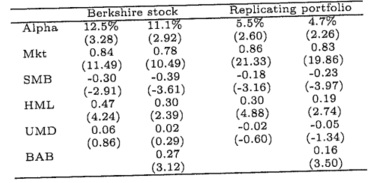
d. In a separate study, the same authors try to understand the investment strategy that is responsible for the remarkable performance of Warren Buffett by examining the returns of Berkshire Hathaway. The table below shows estimates of alphas and slope coefficients from two models: (i) the four-factor model (Carhart), and (ii) a model that adds the BAB factor described in part (c) to the four-factor model. These two models are estimated for the actual returns of Berkshire Hathaway stock, and for a replicating portfolio that uses Berkshire's portfolio holdings of publicly traded stocks as reported in its SEC disclosures at the end of each quarter. Note that Berkshire Hathaway holds more assets than these public traded stocks but only this part of Berkshire Hathaway's portfolio holdings is publicly observable. Alphas are annualized and expressed in percent (t-statistics are shown in parentheses). Interpret the findings from this test. What can explain the difference between the results on the actual returns of the company and the results on the replicating portfolio?
Assignment 4:
Question 1:
Assume you are a risk-averse investor with a quadratic utility function. The assets available for your investment include 2 risky assets and a risk-free asset with the following information:
• E(rx) = 0.16, σx = 0.20
• E(ry) = 0.12, σy = 0.15
• Risk-free rate = 0.06
• The correlation coefficient between the risky assets x and y is 0
If your risk aversion coefficient is A = 6, what fraction of your wealth should be allocated to T-bills and to each of the risky assets? Find the expected return and the standard deviation of the eventual optimal portfolio you will choose to invest in.
b. You are evaluating the performance of two actively managed funds, A and B. You regress the funds' excess returns on the excess return of the market index, and obtain the following index-model regression results:

The risk free rate over the period is 6% and the average return of the market index is 14%.
(i) Which fund is the best choice if it is the only risky asset you will invest in? Show all your work.
(ii) Which fund is the best choice to be mixed with your existing investment portfolio which includes only the S&P 500 Index Fund? Show all your work.
(iii) Which fund would you choose to combine with several other actively managed funds to form an actively managed stock portfolio? Show all your work.
(iv) Using the information in index model regression estimates for fund A, calculate the correlation coefficient between fund A and the market index
c. Consider the following information about the recent performance of a fund manager who allocates capital among equity, bonds, and cash.

Did the manager outperform or underperform the benchmark? What was the contribu¬tion of security selection to relative performance? What was the contribution of asset allocation to relative performance?
d.What happens to portfolio variance as the number of assets, N, in an equal-weighted portfolio gets large? Explain and show all your work.
Question 2:
In this question, we will consider the effects of currency exposure in international invest¬ments. We consider the situation of an investor whose domestic currency is the USD, and who invests in foreign assets denominated in GBP (the foreign currency). The following notation and conventions apply throughout this question:
• All exchange rates are between the USD and GBP, and are quoted in the number of USD that are equivalent to 1 GBP;
• The initial date for the investment is denoted by t, and the final date (one period later) is denoted by t + 1;
• St is the spot exchange rate that prevails at time t, and is the spot exchange rate
that prevails at time t + 1;
• Ft,t+1 is the forward exchange rate that prevails at time t for one-period contracts, that is, contracts that mature and settle at time t + 1;
• rUSD and rGBP are the one-period interest rates in USD and GBP, respectively, that prevail at time t.
In items (a) and (b), you will consider the relationships between the various exchange rates and interest rates mentioned above.
a. Describe uncovered interest rate parity in detail. In particular, describe under what conditions it holds, and state the relationship that holds between St, St+1, Ft,t+1, rUSD and rGBP in that case. Discuss how you could test uncovered interest parity.
b. Describe covered interest rate parity in detail. State the relationship that holds between St, St+1, Ft,t+1 rUSD and rGBP if covered interest parity holds. Describe in detail the market mechanisms that ensure that deviations from this relationship are eliminated, as well as the assumptions required for these mechanisms to work.
For the remaining items in this question, when you need numeric values of the parameters use the following values: St = 1.60, rUSD = 7% and rGBP = 3%.
c. Compute the value of the forward exchange rate Ft,t+1 that must prevail if covered interest parity holds. Justify your approach.
d. Suppose that at time t the investor expects that the spot exchange rate prevailing at time t + 1 (that is, St+1) is 1.62. Does this investor expect that the GBP will appreciate or depreciate vs. the USD? What is the investor's expected currency return for the GBP from a USD perspective? If the investor is absolutely sure that her expectation for St+1 will hold (that is, if at time t the investor's conditional distribution for St+1 has zero variance), should the investor hedge GBP exposure in her international investment?
e. Discuss the implications of test results of uncovered interest parity for the distribution of returns on the carry trade. How would you implement a carry trade between GBP and USD at time t? Based on Verdelhan and Lustig's work, under what conditions would you expect the carry trade to be profitable?
We now consider a situation in which at time t the investor purchases a stock X traded in the London Stock Exchange and denominated in GBP.
f. Suppose that the investor decides to hedge her initial foreign-currency expo¬sure on stock X. Describe in detail how you would advise the investor to do so using forward contracts, and the limitations of your approach.
g. At time t+1, the investor learns that stock X had a GBP-denominated return of 12% from time t to time t+ 1, and that the realized spot exchange rate St+1 is 1.62. Compute the USD-unhedged and USD-hedged return on stock X from time t to time t + 1, justifying your approach.
Question 3:
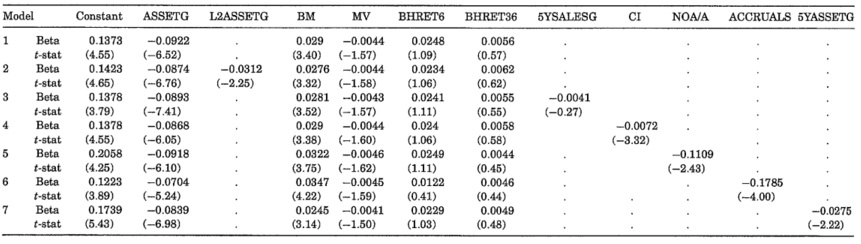
a. In the following table, Cooper, Gulen, and Schill (2008) report Fama-MacBeth regression results where annual stock returns from July 1968 to June 2003 are regressed on lagged accounting and return-based variables. The dependent variable is the annual stock returns calculated from June(t)-July(t+1). ASSETG is the asset growth defined as the percentage change in total assets from the fiscal year ending in calendar year t —2 to fiscal year ending in calendar year t — 1, BM (book-to-market ratio) is calculated using the balance sheet information in the fiscal year ending in calendar year t — 1. MV is the June(t) market value, BHRET6 is the buy-and-hold return over January(t)¬June(t), BHRET36 is the 36-month buy and hold return over July(t-3) to June(t), CI is the measure of abnormal capital investment, L2ASSETG is the asset growth defined as the percentage change in total assets from the fiscal year ending in calendar year t — 3 to fiscal year ending in calendar year t-2, 5YASSETG is a 5-year weighted average rank of asset growth, and 5YSALESG is a 5-year weighted average rank of growth rate in sales. ACCRUALS is from Sloan (1996) and NOA/A is net operating assets divided by total assets. Beta estimates are time-series averages of cross-sectional regression betas obtained from annual cross-sectional regressions (t-statistics are shown in parentheses.)
Interpret the results shown in the table. Why are accounting ratios measured in fiscal year ending in calendar year t —1 for the portfolios formed in June(t)?
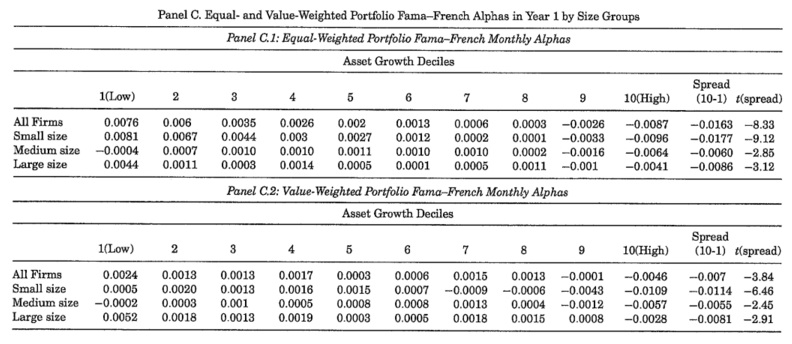
b. The following panels report three-factor alphas of the equal-weighted and value-weighted asset growth portfolios for all firms and for three size-sorted groups. The size groups are defined by ranking firms into one of three groups (small, medium, and large) using the 30th and 70th NYSE market equity percentiles in June of year t. At the end of June of each year t over 1968 to 2002, stocks are allocated into deciles based on asset growth rates defined as the percentage change in total assets from the fiscal year ending in calendar year t - 2 to fiscal year ending in calendar year t - 1. Equal- and value-weighted portfolios are formed based on June(t) asset growth decile cutoffs. The portfolios are held for 1 year, from July of year t to June of year t+1, and then rebalanced. The panels report the monthly alphas in decimal form.
Interpret the results. Why are NYSE breakpoints used in allocating firms into different size categories? What might explain the differences in performance between equal and value-weighted portfolios?
c. The following figure plots the annual buy-and-hold return for equal-weighted portfolios sorted by past asset growth rates. Decile 1 refers to firms in the lowest asset growth decile and decile 10 refers to firms in the highest asset growth decile. The spread is the difference between the returns of the low growth stocks and those of the high growth stocks. What inference(s) can be drawn from the figure regarding the ex-post riskiness of the asset-growth trading strategy?
d. The following figure shows a plot of the average operating margin (EBITDA/Sales) for each asset growth decile over the 5 years before and 5 years after the asset growth sorting year. For example, year 1 shows the operating margin in the year after portfolio formation. Decile 1 is the low asset growth decile, and decile 10 is the high asset growth decile. Is the pattern for operating performance for the extreme asset growth deciles consistent with mispricing explanations for the asset growth anomaly? Explain.
Question 4:
You invest in various sectors in the US equity markets, for which the current market capitalization (in US$ trillion) is as follows:
Sector Market Cap
Information Technology 3.26
Financials 2.87
Health Care 2.38
Consumer Discretionary 2.17
Industrials 1.87
Energy 1.75
Consumer Staples 1.66
Materials 0.61
Utilities 0.51
Telecommunications 0.40
Total 17.5
You also have historical data for the returns of the sector indices. In this question, you will examine the application of the Black-Litterman model to this data.
a. Denote the variance-covariance matrix of ten sector returns as Σ, and the risk-aversion parameter of a representative agent as λ. Carefully explain how the implied market expected returns (denoted by Π) for these sectors are derived. What would your equilibrium sector weights be if you agree with these expected returns? How do the market-implied expected returns and equilibrium weights depend on λ?
b. Now, suppose you have uncertainty regarding the estimate of these sector expected returns, so that your beliefs for expected returns (denoted by p) are captured by the following specification:
μ = Π + εm,
where εm has mean 0 and variance-covariance matrix τΣ. What is the significance of the parameter τ in the Black-Litterman model? How does the introduction of these prior beliefs affect your distribution of returns and optimal portfolio weights?
c. A market strategist you trust has developed some views regarding the future returns of these sectors. They are:
• the Industrials sector will have returns of —2% over the next investment period; and
• the Telecommunications sector will outperform the market-value-weighted average of Utilities and Consumer Staples by 3%. Specify these views in terms of the matrices P and Q.
d. You recognize that there is uncertainty regarding whether your views will prove correct, so that if
Pμ = Q + εv,
you believe that εv is distributed with mean 0 and variance-covariance matrix Ω. Carefully explain how to combine these views with your prior beliefs about fit to update your estimates for expected returns and variance of the returns of these ten sectors, providing explicit expressions for them. Also explain how to compute the resulting optimal weights, and describe qualitatively how you would expect these optimal weights for each sector to differ from those from part (b).
e. Explain in detail the significance of the parameter ft in the Black-Litterman model.
f. You become concerned that the payoffs to the two views you expressed in part (c) are not independent of each other. Instead, you think that the two views are likely to be profitable or unprofitable under similar types of conditions in the equity markets. How would this concern influence your choice of the parameters P, Q and Ω.
g. Suppose that your estimates of the parameters r (from part (b)) and (from part (d)) both doubled from their original values. Explain in detail how you would expect these changes to influence the your posterior estimates of the expected returns and variance of returns. Refer to the expressions for posterior mean returns and variance of returns in your answer.
h. Now, suppose that matrix Ω from part (d) specifically takes the form
Ω = w1 0
0 w2
Holding w2 and τ > 0 constant, describe qualitatively the effect on optimal portfolio weights of letting col vary from a very small (but positive) number to infinitely large. Include a qualitative graph of portfolio weights for any affected sectors in your description.