Calculate the deflection from torsional moment mt and

Question

Problem-1

Pin-connected truss structure is shown in Fig.1. The concentrated forces are applied at E (10,000 lb) and F (15,000 lb). Point A is connected to a solid foundation and B is supported by a roller. Young's modulus E = 10x10⁶ lb/in². As shown in the figure, the total height and length of the structure are 6 ft and 16 ft, respectively.

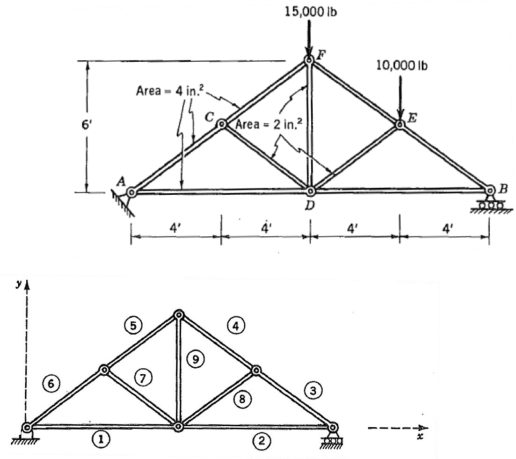
1) Solve the reaction forces (A_x,A_y, B_x, B_y ) at Pont A and B

1-2) Calculate the deflections (δ₁, δ₂, ......δ₉) for all the truss members (indicate if each truss is tensile (+) or compressive (-) with sign

1-3) By applying the virtual forces of P and Q in energy method, calculate the vertical displacement at D and the horizontal displacement at B

Free-Body Diagram should be recalculated with P and Q. Then, contrary to 1-1), an internal force at each member (Fi) is the function of P and/or Q. The horizontal reaction force R3 must be also considered due to Q (Please refer the below figure). For δ at D, Calculate

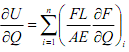Then, apply for P=0. For δ_H at B, Calculate 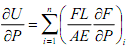Then, apply for Q=0.

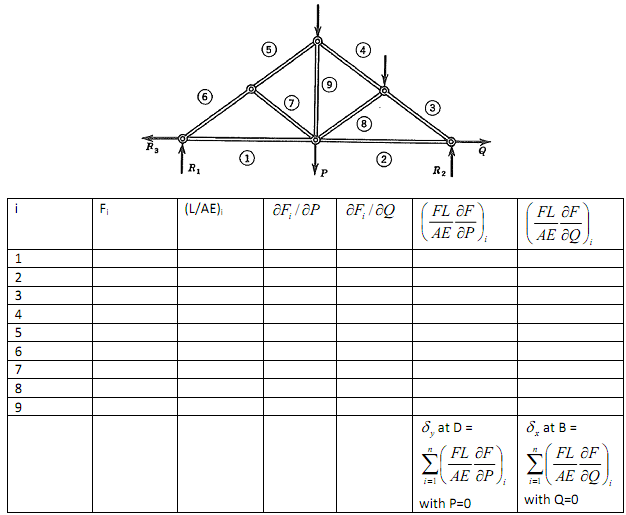
1-4) Now B point is fully supported as shown in the below figure (no movement). Find out the horizontal reaction force of Q and the vertical deflection at D by using Energy method 

Problem-2

2-1) A coil spring with the radius of R is subjected to a load P. The radius of this spring is r and rolled n times.

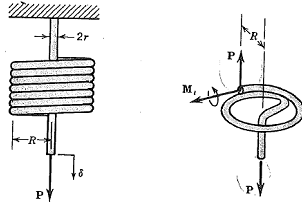
2-1) Define the torsion moment Mt (which is constant through the length and the function of P and R) and derive a formula of the spring deflection of δ by M_t with the function of δ = δ(P, R, G, r, n) using Energy method.

In the above Free-Body Diagram, the deflection by P is ignored. It is assumed that the, torsional moment is only the energy. Then, 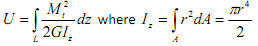and L is the total length of spring under torsion (2ΠRn = Rθ* and dz = Rdθ. By using this relationship, it is convenient to change the integral from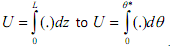

2-2) Calculate spring coefficient k = P/δ and discuss the design on how much spring radius r should be changed to increase k two times

2-3) We consider a coil spring that P is applied at the end (instead of the centre). Calculate the deflection from torsional moment Mt and bending moment Mb and, then discuss the deflection from the torsional moment Mt compared to the result of 2-1)