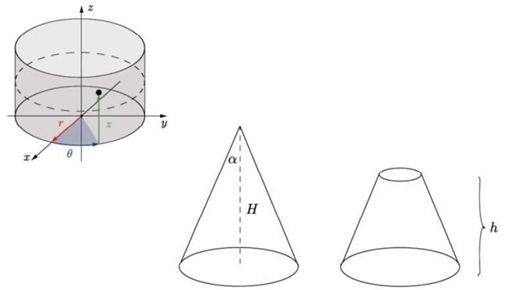
Discuss the below:
Center of mass of cone, cylindrical coordinate system
Q: We are given a cone of height H and angle alpha with constant density. We want to calculate the center of mass using triple integrals in cylindrical coordinates. This requires a description of the solid in such coordinates and the use of the element of volume in the same system of coordinates:
a. Write the element of volume dV in a cylindrical coordinate system.
b. Calculate the Center of Mass of a cone with mass M and height H, and the angle at its head is alpha (or 2 alphas to cover the entire angle of the top). Assume constant density.
c. Now we remove the top from the cone, and its height is now h. What is the center of the mass now?