Assignment:
In the circuit shown below, the switch S is kept in position A for a long time. It is then thrown to position B at a time defined as t = 0
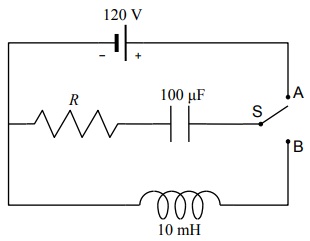
Q1. Calculate the angular frequency ω of the LC oscillations that result when the switch is thrown to position B. What is the frequency f of these oscillations?
Q2. Calculate the time t when the magnitude of the current in the inductor first reaches its maximum value. Justify your answer.
Q3. Calculate the amplitude of the current oscillations. Rather than simply using an equation from the book, try reasoning this out using energy conservation.
Now assume that R takes on a non-zero value. Using energy conservation, describe as quantitatively as possible, what happens to the total energy in the circuit as a function of time. In your discussion, consider the following points:
Q4. What is the initial energy in the circuit?
Q5. Given that the amplitude of the charge on the capacitor decays exponentially as shown by the equation on the cover page, how does the amplitude of the energy stored in the capacitor decay with time?
Q6. If we look at the total energy stored in the circuit as a function of time (that is, the sum of the energy stored in the capacitor and the energy stored in the inductor at any instant), we would observe that it too decreases exponentially over time. Throughout your physics courses, however, you have continually encountered the Principle of Conservation of Energy, which says that the energy of a closed, isolated system must remain constant throughout time. How can we reconcile our observation with this fundamental principle of physics? What can you say about the energy "missing" from the circuit?
. A circuit consists of a battery with emf V, an inductor L, a capacitor C, and two resistors, each with resistance R, as shown in the sketch. The capacitor is initially uncharged and there is no current flowing anywhere in the circuit. The switch S has been open for a long time, and is then closed, as shown in the diagram.
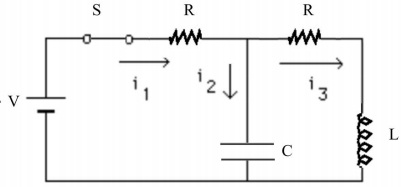
Q7. Using Faraday's Law, what is the sum of the potential drops around the outer loop (the loop including both the battery and the inductor) if we move clockwise around the loop? Note that although we ask you to find this differential equation, you do not have to solve it to answer any later questions.
Q8. Just after the switch S is closed, what are the currents i1, i2, and i3 in terms of the given quantities? Assume that the left loop of the circuit has zero inductance.
Q9. A long, long time after switch S is closed, what are the currents i1, i2, and i3?
Q10. A long, long time after switch S is closed, what is the charge on the capacitor?
Q11. The switch S is now opened again. Just after the switch is opened again, what are the currents i1, i2, and i3 in terms of the given quantities? Assume that the left loop of the circuit has zero inductance.
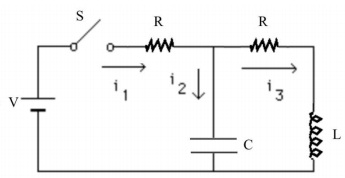
Q12. After approximately how long will the current through the inductor first fall to zero?