Calculate magnitude of tangential component of acceleration

Question

Assignment:

Problems:

1. A stone is thrown straight up with a speed of 25.0 m/s from the top of a building 55.0 m tall.

a. How far above the ground will the stone go?

b. How long until the stone hits the ground?

c. What is the speed of the stone just before it hits the ground?

d. If a ball is thrown downward from the top of the same building with a speed of 25.0 m/s, will its speed just before hitting the ground be greater than, less than, or equal to the speed of the stone just before it hits the ground? Explain. (Hint: What is the speed of the stone when it returns to the height it was thrown?)

2. A ball is thrown from the top of a building of height 40m at an angle of 20° above the horizontal and with an initial speed of 15m/s. Use the assumptions of projectile motion to answer the following questions.

a. How high above the ground will the ball travel?

b. What speed will the ball have at the maximum height?

c. What is the direction of the velocity of the ball at the maximum height?

d. How far has the ball traveled horizontally when it hits the ground?

e. What will be the speed of the ball when it hits the ground?

3. Consider the frictionless system below. The pulley is massless and frictionless, and the string is massless. The mass of each block is m_a = 2.0 kg, m_b = 1.0 kg, m_c = 2.0 kg, and m_d = 1.0 kg.

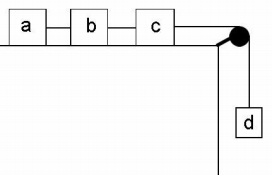
a. What is the acceleration of the system?

b. What is the tension in the string between block a and block b?

c. What is the tension in the string between block b and block c?

d. What is the tension in the string between block c and block d?

e. If the system is initially at rest, how long will it take block d to fall 3.0 m?

4. Two equal masses of 20kg are attached by a massless string and are sliding down an inclined plane of 35°. The coefficients of kinetic friction between the blocks and the ramp are different. The top block has coefficient μ_k1 = 0.700 and the bottom block has coefficient μ_k2 = 0.500. The system accelerates down the plane and the string remains tight.

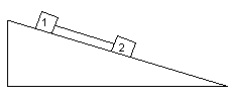
a. Draw a free body diagram for each block.

b. Calculate the tension in the string.

c. Find the magnitude of the acceleration of the blocks.

5. A train slows down as it rounds a sharp horizontal turn, slowing from 25.0 m/s to 13.9 m/s in 15.0 s. The radius of the curve is 150 m.

a. Calculate the magnitude of the tangential component of the acceleration (assumed constant).

b. Calculate the magnitude of the radial component of the acceleration (when the train reaches 13.9 m/s).

c. Calculate the magnitude of the total acceleration (when the train reaches 13.9 m/s).

d. Calculate the angle of the total acceleration vector relative to the radial component (when the train reaches 13.9 m/s)