Calculate and sketch the shear flow distribution and

Question

Q: Your student number is used to assign the values of a and S.

Use the tables below with the last and second last digit of your student number to assign values to a and S respectively.

Last digit n

n	0	1	2	3	4	5	6	7	8	9
a	100	110	120	130	140	150	160	170	180	190

Second last digit m

m	0	1	2	3	4	5	6	7	8	9
S	1000	1100	1200	1300	1400	1500	1600	1700	1800	1900

e.g.: Student number 3308705,   a = 150  (from n = 5),   S = 1000 (from m = 0).

Write your variables on the first page of EACH QUESTION of your solutions.

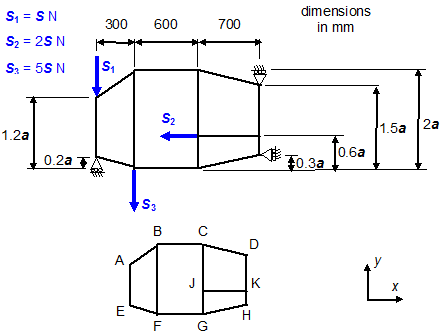
Question 1

The tapered stiffened beam below is loaded by forces S₁, S₂ and S₃ as shown. The beam is assumed to consist of stiffeners carrying only direct stress and shear panels carrying only shear stress. The values of a and S are taken from Question 0.

Calculate and sketch the stiffener axial loads and the panel shear flows.

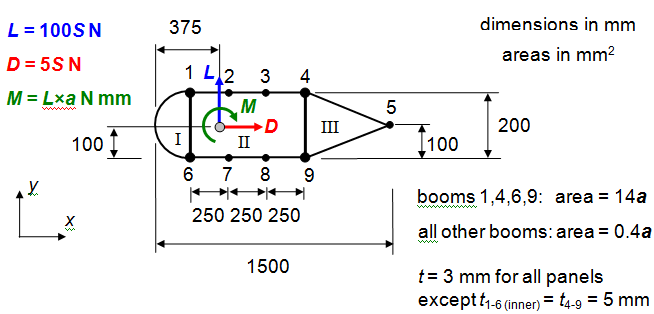
Question 2

The three-cell cross-section shown below uses 9 stiffeners connected with shear panels, where the outer panel between booms 1 and 6 is semi-circular and all other panels are straight. The structure is under the action of forces and moments as shown. Assume the shear panels do not carry any direct stress. The material properties are: E = 72 GPa,
G = 28 GPa, s_ty = 250 MPa, s_cy = 225 MPa, t_y = 150 MPa, n = 0.3. The values of a and S are taken from Question 0.

(a) Calculate and sketch the shear flow distribution and determine the critical margin of safety in shear.

(b) Calculate the critical margin of safety considering shear buckling. Assume that the shear panels are simply supported on all edges, and that the buckling factor K of the curved panel between booms 1 and 6 is 30. The cross-section panels should also be assumed to have infinite length in the out-of-plane (z) direction.