Assignment:
Part 1
1- A metal ball with a mass of 7. 10-6 kg and a charge of +6 mC has a kinetic energy of 2. 108 J. It is traveling directly at an infinite plane of charge with a charge distribution of +5 C/m2. If it is currently 1 m away from the plane of charge, how close will it come to the plane before stopping?
2- A proton gun fires a proton from midway between two plates, A and B, which are separated by a distance of 83.0 cm; the proton initially moves at a speed of 135.0 km/s toward plate B. Plate A is kept at zero potential, and plate B at a potential of 400.0 V.
(a) Will the proton reach plate B?
(b) If not, where will it turn around? (If the proton reaches plate B, enter 0.830 m, the distance between the plates.)
(c) With what speed will it hit plate A? (If the proton reaches plate B, enter 0.)
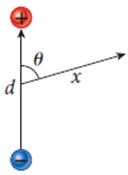
3- Consider a dipole with charge q and separation d. What is the potential a distance x from the center of this dipole at an angle θ with respect to the dipole axis, as shown in the figure? (Do not assume that x » d. Use any variable or symbol stated above along with the following as necessary: k.)
4- Consider an electron in the ground state of the hydrogen atom, separated from the proton by a distance of 0.0529 nm.
(a) Viewing the electron as a satellite orbiting the proton in the electrostatic potential, calculate the speed of the electron in its orbit.
(b) Calculate an effective escape speed for the electron.
(c) Calculate the energy of an electron having this speed. Using this energy, determine the energy that must be given to the electron to ionize the hydrogen atom.
5- An electric field varies in space according to this equation: E = E0xe-x .
(a) For what value of x does the electric field have its largest value, xmax?
(b) What is the potential difference between the points at x = 0 and x = xmax? (State an expression for the difference V(xmax) - V(0).
6- An infinite plane of charge has a uniform charge distribution of +5 nC/m2 and is located in the yz-plane at x = 0. A +24 nC fixed point charge is located at x = +1 m.
(a) Find the electric potential V(x) on the x-axis from 0 < x < +1 m. (Use the following as necessary: x, k, σ for the surface charge distribution, and q and x0 for the charge and position of the point charge, respectively. Do not substitute numerical values; use variables only.)
(b) At what position(s) on the x-axis between x = 0 and x = +1 m is the electric potential a minimum? (Enter your answers from smallest to largest starting with the first answer blank. Enter NONE in any remaining answer blanks.)
7- The electric field, ( ), and the electric potential, V( ), are calculated from the charge distribution, ρ( ), by integrating Coulomb's Law and then the electric field. In the other direction, the field and the charge distribution are determined from the potential by suitably differentiating. Suppose the electric potential in a large region of space is given by V(r) = V0 exp (-r2/a2), where V0 and a are constants and r = x2 + y2 + z2 is the distance from the origin.
(a) Find the electric field ( ) in this region.
(b) Determine the charge density ρ( ) in this region, which gives rise to the potential and field.
(c) Find the total charge in this region.
(d) Roughly sketch the charge distribution that could give rise to such an electric field.
8- Two metal balls of mass m1 = 6 g (diameter = 6 mm) and m2 = 7 g (diameter = 7 mm) have positive charges of q1 = 1 nC and q2 = 8 nC, respectively. A force holds them in place so that their centers are separated by 8 mm. What will their velocities be after the force is removed and a large distance separates them? (Enter the magnitudes of the velocities.)
9- A charge of 0.520 nC is placed at x = 0. Another charge of 0.140 nC is placed at x1 = 10.9 cm on the x-axis.
(a) What is the combined electrostatic potential of these two charges at x = 20.1 cm, also on the x-axis?
(b) At which point(s) on the x-axis does this potential have a (local) minimum? (Enter your answers from smallest to largest starting with the first answer blank. Enter NONE in any remaining answer blanks. If you need to use or - , enter INFINITY or -INFINITY, respectively.)
Part 2
1- A spherical capacitor is made from two thin concentric conducting shells. The inner shell has radius r1, and the outer shell has radius r2. What is the fractional difference in the capacitances of this spherical capacitor and a parallel plate capacitor made from plates that have the same area as the inner sphere and the same separation d = r2 - r1 between plates? (Use the following as necessary: r1, r2, and ε0.)
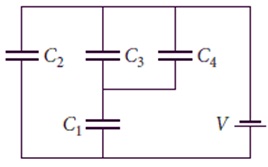
2- Four capacitors with capacitances C1 = 3.4 nF, C2 = 2.2 nF, C3 = 1.6 nF, and C4 = 5.3 nF are wired to a battery with V = 10.3 V, as shown in the figure. What is the equivalent capacitance of this set of capacitors?
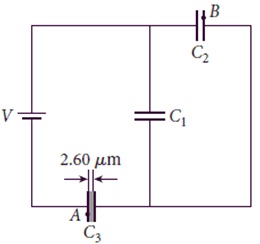
3- A potential difference of V = 80.0 V is applied across a circuit with capacitances C1 = 14.5 nF, C2 = 4.00 nF, and C3= 26.5 nF, as shown in the figure. What is the magnitude and sign of q3l, the charge on the left plate of C3 (marked by point A)? What is the electric potential, V3, across C3? What is the magnitude and sign of the charge q2r, on the right plate of C2 (marked by point B)?
4- Fifty-two parallel plate capacitors are connected in series. The distance between the plates is d for the first capacitor, 2d for the second capacitor, 3d for the third capacitor, and so on. The area of the plates is the same for all the capacitors. Express the equivalent capacitance of the whole set in terms of C1 (the capacitance of the first capacitor).
5- A 7000-nF parallel plate capacitor is connected to a 2.4-V battery and charged.
(a) What is the charge Q on the positive plate of the capacitor?
(b) What is the electric potential energy stored in the capacitor? The 7000-nF capacitor is then disconnected from the 2.4-V battery and used to charge three uncharged capacitors, a 100-nF capacitor, a 200-nF capacitor, and a 300-nF capacitor, connected in series.
(c) After charging, what is the potential difference across each of the four capacitors?
(d) How much of the electrical energy stored in the 7000-nF capacitor was transferred to the other three capacitors?
The Earth is held together by its own gravity. But it is also a charge-bearing conductor.
(a) The Earth can be regarded as a conducting sphere of radius 6371 km, with electric field E = (-150. V/m) at its surface, where is a unit vector directed radially outward. Calculate the total electrostatic potential energy associated with the Earth's electric charge and field.
(b) The Earth has gravitational potential energy, akin to the electrostatic potential energy. Calculate this energy, treating the Earth as a uniform solid sphere. (Hint: dU = -(GM/r)dM. The mass of the Earth is 5.97 1024 kg. Assume that the density of the Earth is uniform.)
(c) Use the results of parts (a) and (b) to address this question: To what extent do electrostatic forces affect the structure of the Earth?
6- A 2.1-nF parallel plate capacitor with a sheet of Mylar (κ = 3.1) filling the space between the plates is charged to a potential difference of 150 V and is then disconnected. (The initial capacitance including the dielectric is 2.1 nF.)
(a) How much work is required to completely remove the sheet of Mylar from the space between the two plates?
(b) What is the potential difference between the plates of the capacitor once the Mylar is completely removed?
7- A proton traveling along the x-axis at a speed of 5.0 106 m/s enters the gap between the plates of a 4.0-cm-wide parallel plate capacitor. The surface charge distributions on the plates are given by σ = ±1.0 10-6 C/m2. How far has the proton been deflected sideways (Δy) when it reaches the far edge of the capacitor? Assume that the electric field is uniform inside the capacitor and zero outside. (The plates of the capacitor are parallel to the x-axis. The charge of the proton is +1.602 10-19 C and the mass of the proton is 1.67 10-27 kg.)