1. Consider the following sampling scheme: randomly permute the N units of a population. The sample a consists of the first n units from the permuted list. Show that this leads to a SRS sampling scheme.
2. A SRS sample a1 of size n1 is selected from a population U of size N. Then another SRS sample a2 of size n2 is selected from a1. Show that a2 is a SRS of size n2 selected from U.
3. Select a SRS a1 of size n1 from a population U of size N. Then from U - a1 select a SRS a2 of size n2. The final sample is a = a1 [ a2. Show that a is a SRS of size n selected from U. What is interesting about this result?
4. Consider the following sampling design for a population of size N = 3, U = {1, 2, 3}:
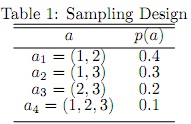
(a) Calculate all the first and second order inclusion probabilities.
(b) Find the value of E[n(a)] in two ways:
(i) by a direct calculation, using the definition;
(ii) by use of the formula that expresses E[n(a)] as a function of the first order inclusion probabilities.
5. A SRS sample a of n individuals is drawn from a frame that lists N individuals. The households corre- sponding to selected individuals are identified. Compute the inclusion probability of a household composed of M individuals, where M < n. Obtain approximate expressions for the inclusion probability for M = 1; 2; 3; assuming that both N and n are large with n=N = f > 0: Think of a situation when such a sampling design could be useful.