By applying the given boundary conditions i need three

Question

Problem

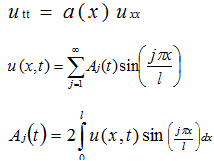
Differentiating the above equation with respect to t twice and using Equation 1 leads to:

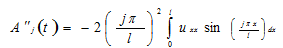
Integrating the first integral on the right-hand side by parts twice yields:

After applying the boundary conditions the above equation simplifies to:

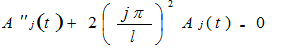
The above equation is now a simple constant coefficient second-order differential equation. The boundary conditions are given by:

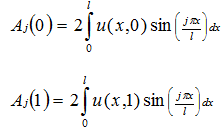
The second order differential equation can be solved analytically.

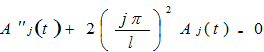
REQUIREMENTS

By applying the given boundary conditions, I need three cases solved analytically for the second order differential equation above.

1. First case

2( jΠ/l )² ≈ 0

2. Second case

2( jΠ/l )² > 0

3. Third case

2( jΠ/l )² < 0

Each case will have a solution.

All the solution steps for the each case explaining how each step was made.