Assignment:
Question 1. A product’s failure time follows the Weibull distribution with the CDF:
F(t) = 1-exp (-(t/η)β)
Where η and β are the parameters. Suppose we know that β = 2 and the prior Distribution of ?? is given by η~exp (?? = 5). After observing three actual failures at 0.25, 0.45, and 0.6, we want to find the posterior distribution of ??. Give the Expression for the posterior distribution and simplify as much as possible (but you do not need to find the final numerical solution).
Question 2. Suppose three experts estimated the failure rate of a product as 10¯³ /year, 10¯³?5/year, and 10¯²?75 /year. We assume these experts are independent and equallygood. If 2 components are tested, with one component failing after 10 months and one component surviving for a year, calculate the point estimate of failure rate ??of this produce after pooling, all the available information using a Bayesian approach.
Question 3. For the system shown below where each labeled box indicates a valve that is Normally open:
(a) Draw a fault tree for the top event “no flow out of the system.”
(b) Find the minimal cutsets.
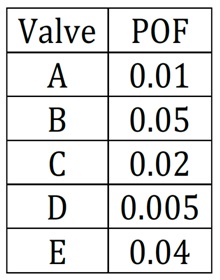
(c) Find the exact top event probability using the basic event probabilities given.
Note: Solve this by expanding the probability of the union of the minimal cutsets
(d) Find the exact top event probability using the basic event probabilities given.
Note: Solve this by drawing the BDD
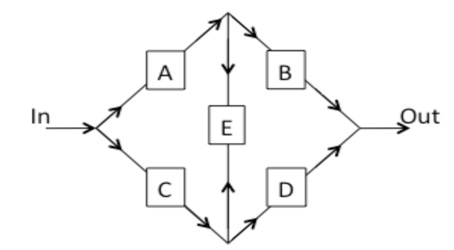
*Note: Flow can go either direction through Leg E, but only one direction in all otherlegs.
Please review the document enclosed here:
Attachment:- Bayesian Analysis-Procedure.rar