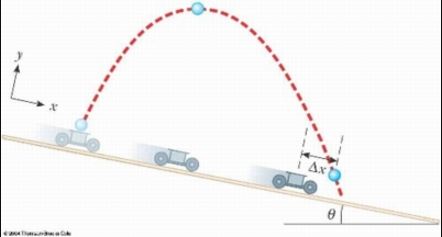
Assignment:
In a demonstration known as the ballistics cart, a ball is projected vertically upward from a cart moving with constant velocity along the horizontal direction. The ball lands in the catching cup of the cart because both the cart and ball have the same horizontal component of velocity. Now consider a ballistics cart on an incline making an angle with the horizontal as in the figure below. The cart (including wheels) has a mass M and the moment of inertia of each of the four wheels about its axle is mR^2/2.
(a) Using conservation of energy (assuming no friction between cart and axles), and assuming pure rolling motion (no slipping), show that the acceleration of the cart along the incline is
Ax = [M/(M + 2m)] g sin (theta)
(b) Note that the x component of acceleration of the ball released by the cart is g sin theta. Thus, the x component of the cart's acceleration is smaller than that of the ball by the factor M/(M + 2m). Use this fact and kinematic equations to show that the ball overshoots the cart by an amount x, where
change in x = [4m/(M + 2m)] [sin theta/cos^2 theta] Vyi^2/g
and
Vyi is the initial speed of the ball imparted to it by the spring in the cart.
(c) Show that the distance d that the ball travels measured along the incline is
d = [2Vyi^2/g] [sin theta/cos^2theta]