Assignment:
Consider the following two-player zero-sum game.
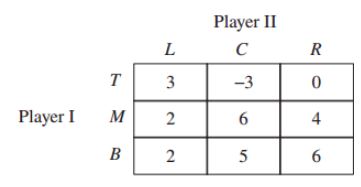
(a) Find a mixed strategy of Player I that guarantees him the same payoff against any pure strategy of Player II.
(b) Find a mixed strategy of Player II that guarantees him the same payoff against any pure strategy of Player I.
(c) Prove that the two strategies you found in (a) and (b) are the optimal strategies of the two players.
(d) Generalize this result: Suppose a two-player zero-sum game is represented by an n × m matrix.4 Suppose each player has an equalizing strategy, meaning a strategy guaranteeing him the same payoff against any pure strategy his opponent may play. Prove that any equalizing strategy is an optimal strategy.
(e) Give an example of a two-player zero-sum game in which one of the players has an equalizing strategy that is not optimal. Why is this not a contradiction to (d)?
Provide complete and step by step solution for the question and show calculations and use formulas.