Amplitude-phase-shift-period-and equation of midline

Question

1. Solve the subsequent functions for x (where x is a real number). Leave your answers in precise form,

(a) 3^x3^x23^x3 = 3^31x

(b) 4e^2x = 21 − e^4x

(c) log₂(x − 10) + log₂(x) = log₂(119)

2. A manager has determined the cost C, in dollars, for manufacturing is

C(q) = 85 log₁₀ (10 + q/2)

for manufacturing, where q is the number of units produced in a given day.

(a) What is cost of manufacturing before any units are produced?

(b) What is cost of manufacturing if 1980 units are produced in a given day?

(c) How many units would be produced if the cost of manufacturing is $150 in a given day?

3. Find out all solutions of the following equations in the interval [0, 2 π)

(a) sin(2x) =√2 cos(x).

(b) 2 cos²(x) + 3 sin(x) = 3.

4. (a) Sketch the graph of the circular function

f(θ) = 1 − 2 cos(3θ + π)

i. State clearly the amplitude, phase shift, period and the equation of the midline.

ii. Show working for all θ- and y-intercepts for the function y = f(θ).

iii. Show at least two periods for the graph of y = f(θ), and label the axes clearly.

(b) Prove the following identity

2 sin(1/2(x + y)) cos (1/2(x − y)) = sin(x) + sin(y) .

Make sure you demonstrate all working and give clear explanations.

5. Consider the function

f(x) = ½ (2^x + 2^−x)

which has the graph

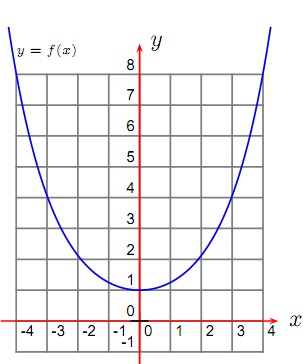
(a) Elucidate why f has no inverse function. You must include an example to support your explanation.

(b) Determine the largest possible domain, which includes x = 1, for f(x) such that the inverse function f^-1(x) does exist.

(c) Given your answers in (b) find the inverse function f^-1(x). Clearly elucidate key steps and show all working.

(d) Sketch the graph of y = f(x) for the restricted domain in (b) and y = f^-1(x) on the same set of axes. All points of intersection and axes-intercepts should be easily determined from your sketch or clearly labeled. Furthermore axes must be clearly labeled with appropriate scaling.