Questions:
Tables and Seats
1. Do the problem "Tables and Seats" in this topic. As you work on the problem, see if you can arrive at your solution from several different approaches. Upload your completed solution and methods.
2.Reflect on the aspects of algebraic thinking you discovered in the problem that were applicable to your problem-solving strategies. What algebraic thinking did you engage in when solving this problem? ( at least 200 words)
Tables and Seats
A certain restaurant has square tables that can seat four people each. So on a normal day, one table will seat four people, two tables will seat eight people, etc.
You and your 11 friends (12 of you total) would like to go eat together at the restaurant, so you call ahead to make sure there are enough tables. The manager tells you he will need to put the square tables together in a row banquet-style to seat all of you.
"Great," you say, "Each table seats four people, so that means you'll need 3 tables, since 3 x 4 = 12."
"Not quite," says the manager. "I'll need more than that."
Use square tiles to explore what happens when you put together two square tables in a row.
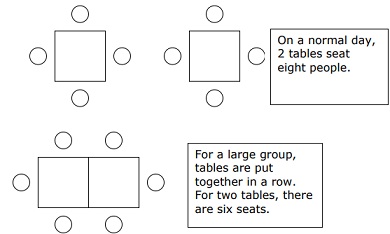
1. How many tables will the manager need to put together to seat all 12 of you?
2. How many tables for a group of 18 people?
3. How many seats would 20 tables have?
4. Can you determine the number of seats for any number (n) of tables?
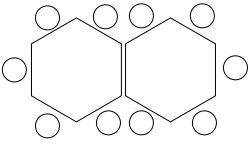
Now try exploring the restaurant next door, which uses hexagonal tables with 6 seats. Let’s say you need seats for 22 people. How many tables will you need?How many seats will n tables have?
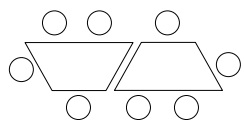
How about a trapezoid table which usually seats 5 people? Predict the number of seats for n number of tables
Here's an interesting extension: Students should notice that the formulas derived from the different tables are similar. See if you can find an even more general formula with two variables: N representing the number of tables and S representing the number of seats per single table