Absolute value of the heat of reaction

Question

Directions: Show all work and assumptions. Cite sources where appropriate. Engineering software must be used for all calculations, with the code/analysis submitted. The code/analysis must be thoroughly commented. Box or highlight final answers.. If a part cannot be solved, state an assumed value and move on if necessary.

Givens:

M_∞      Th, Thrust (kN)      H, Altitude (km)       TF (%)            M₂       h₅ (cm)       M_engine (kg)

2.9              65                         11                     80              0.23         18                   55

η_b               r_n                         PR_n               δ1= δ2, (°)

0.99           0.98                      1.02                    15

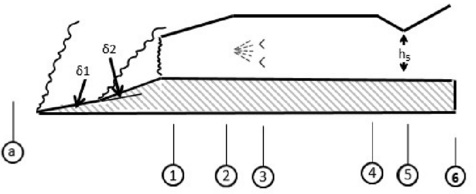
Part I: A simple, rectangular ramjet is to be designed, to propel an aircraft at a flight Mach number of M_∞. Supersonic compression is carried out by a system of 2 oblique shocks followed by a normal shock. Ramp deflection angles (δ) are equal. It is known that Th kN of thrust is required for cruise conditions, at an altitude of H km. At this altitude, the exhaust nozzle is perfectly expanded. The nozzle throat height is h5 cm, as shown. It is to be fueled with Methane (MW=16.04g/mol), and is allowed a maximum temperature of TF% of the stoichiometric, adiabatic flame temperature (ie T_max=TF% * T_AF). Assume that the reactants are at 300K for the calculation of T_AF. The flow will be decelerated to a Mach number of M2 at the inlet of the combustor. The engine's empty mass will be M_engine kg. The conceptual design is shown below.

For the real engine analysis, the combustion efficiency is η_b, the stagnation pressure ratio across the nozzle is r_n. The nozzle is also slightly under expanded, where P₆/P_a=PR_n.

Considering an ideal ramjet (no shock, no losses), and assuming the propellant can be treated as air with γ=1.4,

C_p=1005 J/kg-K, and R=287 J/kg-K. Determine:

a) The absolute value of the heat of reaction (Q_R in kJ/kg) for the fuel. Assume an idealized, low temperature, stoichiometric combustion process in air.

b) The required fuel air ratio to achieve the maximum temperature, T_max.

c) The required air mass flow through the engine.

d) The required fuel mass flow.

e) The width (normal to the page) of the engine, such that station 5 is choked.

f) Height at station 6, assuming Pe=Pa (ie perfectly expanded)

g) The TSFC, η_p, η_th, η_o,

For the real ramjet, determine:

h) The stagnation pressure ratio across the diffuser (rd), neglecting friction and heat loss (ie. Only account for the shock system).

i) The stagnation pressure ratio across the combustor (rc), neglecting friction and area change, and only accounting for the change in total temperature.

Part II: Rather than a ramjet, it is proposed to utilize a turbojet for the same cruise conditions (altitude & flight Mach number).

a) Design an ideal turbojet cycle for this application, making realistic assumptions. Utilize JP4 as the fuel. Report assumed engine operating conditions (compressor pressure ratio, T04)

b) Determine the required air mass flow through the engine

c) Determine the fuel mass flow required

d) Determine the TSFC, η_p, η_th,

Part III: Plot both ideal cycles on a TS diagram using MATLAB, Excel, or a similar software. Compute entropy, temperature, and pressure at all stations. Label all stations.