1a state the limit denition of the derivative fxb

Question

1.

(a) State the limit de?nition of the derivative f'(x).

(b) Using the limit de?nition of the derivative, compute f'(x) when f (x) = x².

(c) Find the equation of the tangent line to the graph of y = x² when x = 2.

2. Solve the following equations. When applicable, write your answer in interval notation.

(a) log(2x 3) = 0 (Write your answer as a whole number.)

(b) e^_ex= 4

(c) |2x 1| > 5

(d) x² + 2x ≤ 3

3. Evaluate the following limits and justify your answer. DO NOT use L'Hospital's rule.

(a) lim _x->Π4tan(x)

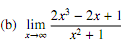
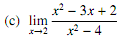
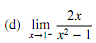
4. The position of a particle moving along a straight line is given by

s(t) = 2t³+ 3t² - 12t

(a) Find the velocity and the acceleration of the particle.

(b) Determine when the particle is moving forward (i.e. in the positive direction) and when the particle is moving backward (i.e. in the negative direction). Write your answer in interval notation.

(c) Sketch the motion of the particle on the line below, and ?nd total distance traveled by the particle after time t = 2.

5. (a) Dierentiate: f (x) = (x³ + 1)¹⁰

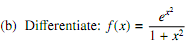
(c) Find y' if cos(xy) = 1 + sin(y).

(d) Dierentiate via logarithmic dierentiation: f (x) = x^log(x)

6. A spherical snowball melts so that its surface area decreases at a rate of 4 cm² min. Find the rate at which the diameter decreases when the diameter is 10 cm. (The surface area of a sphere of radius r is S = 4Πr²)