(1) Prove the following vector calculus identity in R3, where f is a twice continuously di erentiable scalar eld and F is a twice continuously di erentiable vector fi eld:
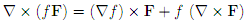
(2) Let F(x; y; z) = (y + z)i + (x + z)j + (x + z)k. The sphere x2 + y2 + z2 = a2 intersects the postive x-, y-, and z-axes at points A, B, and C, respectively. The simple closed curve K consists of the three circular arcs AB, BC, and CA. Let S denote the surface ABC of the octant of the sphere bounded by K, oriented away from the origin. Let T denote the unit tangent vector to K, and n the unit normal vector to S.
(a) Calculate the line integral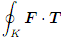 
ds directly without using Stokes' Theorem.
(b) Calculate the surface integral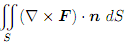 
without using Stokes' Theorem.
(3) Consider the matrix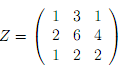 
(a) Find a PLU decomposition for the matrix Z.
(b) Use your answer to part (a) to solve the system of equations
x + 3y + z = 1;
2x + 6y + 4z = 4;
x + 2y + 2z = 6:
(4) Consider the matrix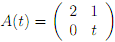 
(a) Find the eigenvalues and eigenvectors of A(t).
(b) For which values of t will A(t) be diagonalisable? Explain.
(c) For those values of t from part (b), nd an invertible matrix P(t) and a diagonal matrix D(t) such that A(t) = P(t)D(t)P(t)-1.
(d) Give a formula for A(t)n (where n is a positive integer) that holds for those values of t from part (b).