1. Consider the function f de?ned by
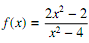
The ?rst and second derivatives of f are
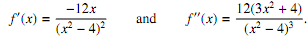
(a) Determine the domain of f . Write your answer in interval notation.
(b) What are the x-intercept(s) of the graph of f ? What are the y-intercept(s) of the graph of f ?
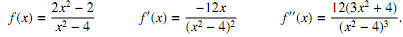
(c) Find each horizontal asymptote of the graph of f , if any exists, by using the limit de?nition of horizontal asymptote.
(d) Find each vertical asymptote of the graph of f , if any exists, by using the limit de?nition of vertical asymptote.
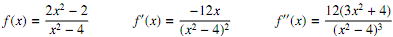
(e) Find where f is increasing, and where f is decreasing? Write your answer in interval notation.
(f) Find critical points of f and classify each as a local maximum, a local minimum, or neither.
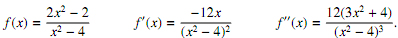
(g) Determine where the graph of f concave up, and where the graph of f concave down? Write your answer in interval notation.
(h) sketch the graph f.
2. (a) Find the linearization of f (x) = (x + 1)4 at a = 1, and use it to approximate (2.01)4
(b) Evaluate 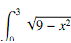 dx by interpreting it in terms of areas. In other words, draw a picture of the region the integral represents, and ?nd the area using high school geometry.
dx by interpreting it in terms of areas. In other words, draw a picture of the region the integral represents, and ?nd the area using high school geometry.
3. Evaluate the following limits using L'Hospital's Rule.
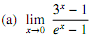
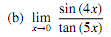
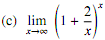
4. Di�erentiate the following functions.
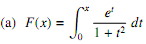
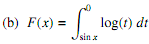
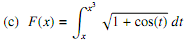
5. Evaluate the following de?nite integrals.
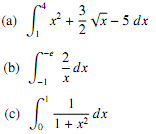
6. A farmer wants to fence o� a rectangular ?eld and then divide the ?eld in half with a fence down the middle (see diagram below). If he can only a�ord 240 ft. of fencing material, what is the width y which gives the maximum area of the ?eld?