--%>
Assignment Help - homework help

What is Elevation in boiling point?

The boiling of a liquid may be defused by the temperature at which its vapour pressure which is equal to atmospheric pressure. The effect of addition in a non-volatile solute on the boiling point shown and its solution containing non-volatile solute with temperature are represented by the curves AB and CD respectively. It is evident by the curves temperature the vapour pressure of solutions is lower than that of the pure solvent and thus, the vapour pressure.

Curve for solution runs below that of the pure solvent. At temperature T0, the vapour pressure of the pure solvent becomes equal to the atmospheric pressure. Thus, the atmospheric pressure and therefore, it is necessary to heat the solution to a higher temperature sayT1 in the atmospheric pressure. Thus, it is clear that the solution in higher temperature than the pure solvent. Evidence T1 - T0 (or Δ Tb)is the elevation in boiling point vapour pressure (Δp), the elevation in the boiling point is also proportional to the solute concentration. Thus,

ΔTb ∝ Δp

According to Raoult's law, Δp ∝ xB

∴ ΔTb ∝ xB

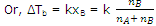
1444_elevation in boiling point.png 

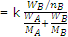
1084_elevation in boiling point1.png 

1730_elevation in boiling point2.png 

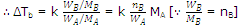
1333_elevation in boiling point3.png 

If WA is the mass of solvent in kg, then 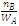 1283_elevation in boiling point4.png is equal to molality (m) of the solution

ΔTb = kMA m

Here, k and MA are constants and hence their product, i.e. kMA is replaced by another constant K2.

ΔTb = Kb m, where Kb is called boiling point-elevation constant or molal elevation constant or molal ebullioscopic constant.

As elevation in boiling point depends upon the relative number of moles of solute and solvent but does not depend upon the nature of solute, so it is a colligative property.

   Related Questions in Chemistry

  • Q : What is solvent dielectric effect?

    Ionic dissociation depends on the dielectric constant of the solvent.The Arrhenius that ions are in aqueous solutions in equilibrium with parent molecular species allows many of the properties of ionic solutions to be understood. But difficulties began to

    		•
  • Q : Organic and inorganic chemistry Write

    Write down a short note on the differences between the organic and inorganic chemistry?

    		•
  • Q : Number of moles of potassium chloride

    Choose the right answer from following. The number of moles of KCL in 1000ml of 3 molar solution is: (a)1 (b)2 (c)3 (d)1.5

    		•
  • Q : Problem based on molarity Choose the

    Choose the right answer from following. The molarity of a solution of Na2CO3 having 10.6g/500ml of solution is : (a) 0.2M (b)2M (c)20M (d) 0.02M

    		•
  • Q : Coagulation what is the meaning of

    what is the meaning of fourth power of valency of an active ion?

    		•
  • Q : Problem on mole fraction of glucose

    Provide solution of this question. While 1.80gm glucose dissolve in 90 of H2O , the mole fraction of glucose is: (a) 0.00399 (b) 0.00199 (c) 0.0199 (d) 0.998

    		•
  • Q : Molarity what is the molarity of the

    what is the molarity of the solution prepared by dissolving 75.5 g of pure KOH in 540 ml of solution

    		•
  • Q : Determining mole fraction of water in

    A mixture has 18 g water and 414 g ethanol. What is the mole fraction of water in mixture (suppose ideal behaviour of mixture): (i) 0.1  (ii) 0.4  (iii) 0.7  (iv) 0.9 Choose the right answer from abo

    		•
  • Q : Why acetic has less conductivity than

    Illustrate the reason, why acetic has less conductivity than Hcl?

    		•
  • Q : Liquid Vapour Free Energies The free

    The free energy of a component of a liquid solution is equal to its free energy in the equilibrium vapour.Partial molal free energies let us deal with the free energy of the components of a solution. We use these free energies, or simpler concentration ter

    		•