--%>
Assignment Help - homework help

What is depression in freezing point?

Freezing point of a substance is the temperature at which solid and liquid phases of the substance coexist. It is defined as the temperature at which its solid and liquid phases have the same vapour pressure.

The freezing point of a pure liquid is preset. Now, if a non-volatile solute is dissolved in the pure liquid to constitute a solution, there occurs a lowering in the freezing point. The freezing point of solution refers to the temperature at which the vapour pressure of the solvent in two phases, i.e. liquid solution and solid solvent is the same. Since the vapour pressure of the solvent at a lower temperature.

Evidently the freezing point of the pure solvent is the temperature corresponding to the point B (T0 K) and that of the solution is the temperature corresponding to the point A'(T1 K). Clearly, (T0 - T1) or ΔTƒ is the freezing point depression. Since its magnitude is determined by that of lowering of vapour pressure, the freezing point depression depends upon the molal concentration of the solute and does not depend upon the nature of solid. It is, thus, a colligative property. The general relation between these two quantities for a solution of non-electrolyte is usually expressed in term of molality of the solution

ΔTƒ ∝ Δp and Δp ∝ xB

∴ ΔTƒ = kxB =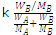415_freezing point.png 


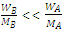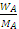For dilute solution, 272_freezing point1.png   and hence,1964_freezing point2.png.


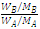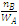∴ ΔTƒ = k 1278_freezing point3.png  = k582_elevation in boiling point4.pngMA


If WA is the mass of solvent in kg, then   is equal to molality (m) of the solution

ΔTƒ = kMAm     (? kMA = Kƒ)

∴ ΔTƒ =Kƒm, where Kƒ is called Freezing point depression constant or molal depression constant or cryoscopic constant.

As is clear from the above, depression in freezing point depends upon relative number of moles of solute and solvent but does not depend upon nature of solute, so it is a colligative property.

   Related Questions in Chemistry

  • Q : Describe Point Groups. For any

    For any symmetric object there is a set of symmetry operations that, together, constitute a mathematical group, called a point group.It is clear from the examples that most molecules have several elements of symmetry. The H2O

    		•
  • Q : Entropy is entropy on moleculare basis

    is entropy on moleculare basis relates to the tras.,vib.,and rotational motions?

    		•
  • Q : Basic concepts Determination of correct

    Determination of correct mol. Mass from Roult's law is applicable to :

    		•
  • Q : Degree of dissociation The degree of

    The degree of dissociation of Ca(No3)2 in a dilute aqueous solution containing 14g of the salt per 200g of water 100oc is 70 percent. If the vapor pressure of water at 100oc is 760 cm. Calculate the vapor pr

    		•
  • Q : Problem on bubble point The following

    The following mixture of hydrocarbons is obtained as one stream in a petroleum refinery.

    Q : What are methods of phenol preparation

    Phenol was initially obtained by fractional distillation of coal

    		•
  • Q : What are emulsions?Describe its

    Emulsions are colloidal solutions in which disperse phase as well as dispersion medium is both liquids. Emulsions can be broadly classified into two types: (i) Oil in water (O/W type) emulsions: in this type of emulsions, oil acts disperse phase and water acts

    		•
  • Q : Define alum Illustrate alum?

    Illustrate alum?

    		•
  • Q : Explain the molecular mass with respect

    During the formation of polymers, different macromolecules have different degree of polymerisation i.e. they have varied chain lengths. Thus, the molecular masses of the individual macromolecules in a particular sample of the polymer are different. Hence, an average value of the molecular mass is

    		•
  • Q : What do you mean by the term alum What

    What do you mean by the term alum? Also illustrate its uses?

    		•