--%>
Assignment Help - homework help

Solution Of Laplace’s Equation

1. Solve Laplace's equation for the electrical potential between two infinite parallel plates, which have a charge density per unit area -on one plate and a charge density per unit area -! on the second plate, and determine the electric field between the plates from the potential. (You should use the fact that for plates of infinite area, the potential only depends on distances perpendicular to the plates. (Since the object of this problem is to solve Laplace's equation for a problem for which you already know the electric field, if all that you do is to quote the value for the electric field that you already know from Gauss's law, without solving Laplace's equation, you will receive no credit.)

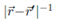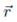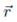2. The Coulomb potential 1853_123.pngcan be written as r-1F(u, x), where F(u, x) = [1 - 2ux + u2]-1/2, where u = r!/r and x = cos Θ, where Θ is the angle between 1928_1234.pngand 1928_1234.png. Expand F(u, x) up to third order in u, and by doing so, demonstrate that the Taylor series for F(x, x), as a function of u,

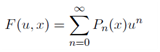
2472_12341323.png

is valid to third order in u. (Therefore,

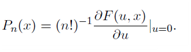
1810_54444.png

Incidentally, F(u, x) is known as the generating function for the spherical harmonics because its derivatives are proportional to the spherical harmonics.)

3. A point dipole is placed at the center of a grounded spherical conducting shell. Find the resulting potential inside the shell, (Hint: You must add to the expression for the potential due to a point dipole solutions to Laplace's equation that do not diverge at the center of the sphere, which we will assume to be the origin of coordinates.)

4. A long cylindrical conductor is placed in an initially (i.e., before the cylinder is present)uniform electric field which is perpendicular to the axis of the cylinder.

a) Find the electrical potential outside of the cylinder.

b) Find the surface charge density on the cylinder.

c) What is the electrical potential inside the cylinder when it is in the electric field.

   Related Questions in Physics

  • Q : Define Noether theorem Noether theorem

    Noether theorem (Noether): A theorem that explains that symmetries are what gives rise to conserved quantities. For example, the translational symmetry (that is the fact that the laws of physics work the same in all positions) gives r

    		•
  • Q : Describe the term Specular Reflection

    Describe briefly the term Specular Reflection?

    		•
  • Q : Define Spin-orbit effect Spin-orbit

    Spin-orbit effect: The effect that causes atomic energy levels to be split since electrons contain intrinsic angular momentum (that is spin) in summation to their extrinsic orbital angular momentum.

    		•
  • Q : Balanced field takeoff Describe the

    Describe the process of balanced field takeoff in brief?

    		•
  • Q : Define Hoop conjecture Hoop conjecture

    Hoop conjecture (K.S. Thorne, 1972): The conjecture (as so far unproven, although there is substantial proof to support it) that a non-spherical object, non-spherically compressed, will only form a black hole whenever all parts of the

    		•
  • Q : What is Wiens displacement law constant

    Wien's displacement law constant, b: It is the constant of Wien displacement law. This has the value of 2.897 756 x 10-3 m K.

    		•
  • Q : Atomic model which the Erwin

    Briefly state the atomic model which the Erwin Schrodinger creates?

    		•
  • Q : Water drain contradict problem Does

    Does water drain contradict clockwise in the northern hemisphere and clockwise in the southern hemi-sphere? Briefly explain it.

    		•
  • Q : What is Hooke law Hooke's law (R.

    Hooke's law (R. Hooke): The stress exerted to any solid is proportional to the strain it generates within the elastic limit for that solid. The constant of that proportionality is the Young modulus of elasticity for that material.

    		•
  • Q : Procedure to define the Specific Gravity

    Briefly explain the procedure to define the Specific Gravity?

    		•