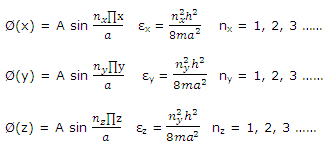--%>
Assignment Help - homework help

Schrodinger equation with particle in a box problem.

Three dimensional applications of the Schrodinger equation are introduced by the particle-in-a-box problem.

So far only a one-dimensional problem has been solved by application of the Schrodinger equation. Now the allowed energies and the probability functions for a particle that is free to move in three dimensions are deduced. A molecule of a gas enclosed in a cubic container provides a specific example that is dealt with in the section after the general procedure has been developed.

For any three-dimensional problem, the potential energy is, general, a function of three coordinates. For a cubic potential box, the Cartesian coordinates are convenient. The differential equation that must be solved is now the Schrodinger equation in three dimensions.

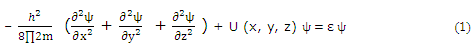
1310_Particle in a box.png 

For a "cubic box," the potential function can be expressed in terms of separate x, y, and z components,
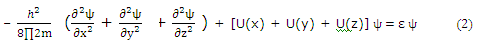
98_Particle in a box1.png 

Each of the potential function components for a "particle-in-a-box" is like the one-dimensional potential for a "particle-on-a-line".

For three-dimensional systems, the solution function ψ depends on the three coordinates necessary to locate a point in space. It is often profitable to try to separate such systems into parts, with each part involving only one coordinate. On the basis we try the substitution

ψ (x, y, z) = Ø(x)Ø(y)Ø(z)

Substitution of (2) from (1) gives

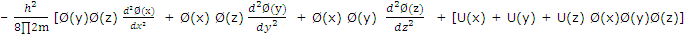
1350_Particle in a box2.png 

Division by Ø(x)Ø(y)Ø(z) gives

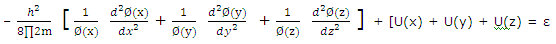
1180_Particle in a box3.png 

For the equation to be satisfied for all values of x, y and z, each term on the left must equal a component of ε, and we can write

ε = εx + εy + εz

The Schrodinger equation can then be broken down into three identical equations of the type

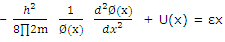
1394_Particle in a box4.png 

Or

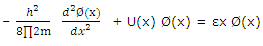
578_Particle in a box6.png 

These equations are identical to that written for one-dimensional problem. The solution to the three-dimensional cubic-box problem is therefore

ψ =  Ø(x)Ø(y)Ø(z)

With

1809_Particle in a box7.png

   Related Questions in Chemistry

  • Q : Molarity of Barium hydroxide 25 ml of a

    25 ml of a solution of barium hydroxide on titration with 0.1 molar solution of the hydrochloric acid provide a litre value of 35 ml. The molarity of barium hydroxide solution will be: (i) 0.07 (ii) 0.14 (iii) 0.28 (iv) 0.35

    		•
  • Q : Procedure for separating the components

    Briefly describe the procedure for separating the components of the gun-powder?

    		•
  • Q : Finding strength of HCL solution Can

    Can someone please help me in getting through this problem. 1.0 gm of pure calcium carbonate was found to require 50 ml of dilute  HCL for complete reaction. The strength of the HCL  solution is given by: (a) 4 N  (b) 2 N  (c) 0.4 N  (d) 0.2 N

    		•
  • Q : Unit of molality Select the right

    Select the right answer of the question. The unit of molality is: (a) Mole per litre (b) Mole per kilogram (c) Per mole per litre (d) Mole litre

    		•
  • Q : Describe Transformation Matrices. Each

    Each symmetry operation can be represented by a transformation matrix.You have seen what happens when a molecule is subjected to the symmetry operation that corresponds to any of the symmetry elements of the point group to which the molecule belongs. The m

    		•
  • Q : Number of moles of potassium chloride

    Choose the right answer from following. The number of moles of KCL in 1000ml of 3 molar solution is: (a)1 (b)2 (c)3 (d)1.5

    		•
  • Q : Question based on vapour pressure and

    Benzene and toluene form nearly ideal solutions. At 20°C, the vapour pressure of benzene is 75 torr and that of toluene is 22 torr. The parial vapour pressure of benzene at 20°C for a solution containing 78g of benzene and 46g of toluene in torr is: (a) 50 (b)

    		•
  • Q : Describe the properties of the

    Briefly describe the properties of the carbohydrates?

    		•
  • Q : Coordination compounds discuss the

    discuss the practical uses of coordination compounds, give reactions involves and explain whats happening in the process

    		•
  • Q : Death cap musrooms the death cap

    the death cap mushroom based on your knowledge of the biochemistry of dna and rna

    		•