--%>
Assignment Help - homework help

Problem on utility funtion probability

Suppose that your utility, U, is a function only of wealth, Y, and that U(Y) is as drawn below. In this graph, note that U(Y) increases linearly between points a and b. 

Suppose further that you do not know whether or not you will be sick, but you do know that the probability of becoming sick is p (while the probability of staying healthy is 1-p).  If you do get sick, your wealth will be Ys = 0.  If you do not get sick, your wealth will be Yh > 0. 

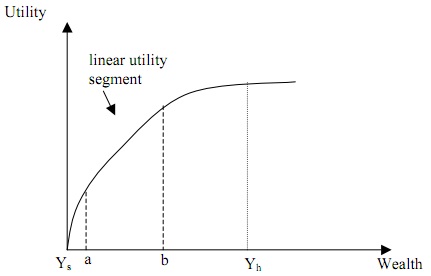
1940_utility function.jpg

(1) Write an expression for expected income, EI, and an expression for expected utility without insurance.
 
(2) Assume that a < EI < b.  Draw, on the graph above, a line showing expected utility without insurance. Also draw a line showing expected utility with actuarially fair full insurance.

(3) Consider an actuarially fair partial insurance contract that offers a if you are sick and b if you are healthy. Would your utility with such a contract be greater or less than your utility with an actuarially fair full insurance contract? Briefly, explain. 

   Related Questions in Advanced Statistics

  • Q : Problem on utility funtion probability

    Suppose that your utility, U, is a function only of wealth, Y, and that U(Y) is as drawn below. In this graph, note that U(Y) increases linearly between points a and b.  Suppose further that you do not know whether or not you

    		•
  • Q : Probability of Rolling die problem A

    A fair die is rolled (independently) 12 times. (a) Let X denote the total number of 1’s in 12 rolls. Find the expected value and variance of X. (b) Determine the probability of obtaining e

    		•
  • Q : Problem on income probability Kramer

    Kramer spends all of his income  $270  on two products, soup (S) and on golf balls (G). He always bought 2 golf balls for every 1 cup of soup he consumes. He acquires no additional utility from the other cup of soup unless he as well gets 2 more golf balls a

    		•
  • Q : Problem on consumers marginal utility

    Consider a consumer with probability p of becoming sick.  Let Is be the consumer’s income if he becomes sick, and let Ins be his income if he does not become sick, with Is < Ins. Suppo

    		•
  • Q : Random variables Random variables with

    Random variables with zero correlation are not necessarily independent. Give a simple example.    

    		•
  • Q : Pearsons correlation coefficient The

    The table below illustrates the relationship between two variable X and Y. A

    		•
  • Q : Analysing the Probabilities 1. In the

    1. In the waning seconds of Superbowl XLVII, the Baltimore Ravens elected to take a safety rather than punt the ball. A sports statistician wishes to analyze the effect this decision had on the probability of winning the game. (a) Which two of the following probabilities would most help t

    		•
  • Q : Use the law of iterated expectation to

    Suppose we have a stick of length L. We break it once at some point X _

    Q : Describe what happens to the confidence

     A nurse practitioner working in a dermatology clinic is studying the efficacy of tretinoin in treating women's post partum abdominal stretch marks.  From a sample of 15 women, the mean reduction of stretch mark score is -0.33 with a sample standard deviation of 2.46.  Describe wha

    		•
  • Q : Find the cumulative distribution

    You must use the pre-formatted cover sheet when you hand in the assignment. Out full detailed solutions. Sloppy work will naturally receive a lower score. 1. Suppose at each step, a particle moving on sites labelled by integer has three choices: move one site to the right with pro

    		•