--%>
Assignment Help - homework help

Problem on Maple

(a) Solve the following  by:

(i) First reducing the system of first order differentiat equations to a second order differential equation.

(ii) Decoupling the following linear system of equations

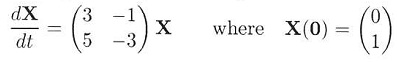
1230_maple.jpg

(b) Using the eigenvalue approach, determine  the asymptotic behaviour of solution for t.

(c) Using Maple:

(i) Check your solution that you have  found in (above) and graph your solution with respect to time.

(ii) Graph the components of X(t) against each other and identify the direction of solution as t → infinity

   Related Questions in Mathematics

  • Q : Where would we be without stochastic

    Where would we be without stochastic or Ito^ calculus?

    		•
  • Q : Define Well-formed formulas or Wffs

    Wffs (Well-formed formulas): These are defined inductively by the following clauses:    (i) If  P  is an n-ary predicate and  t1, …, tn are terms, then P(t1, …, t

    		•
  • Q : Explain a rigorous theory for Brownian

    Explain a rigorous theory for Brownian motion developed by Wiener Norbert.

    		•
  • Q : Problem on mixed-strategy equilibrium

    Assume three Offices (A, B, & C) in downtown,  simultaneously decide whether to situate in a new Building. The payoff matrix is illustrated below. What is (are) the pure stratgy Nash equilibrium (or equilibria) and mixed-strtegy equilibrium of the game?

    		•
  • Q : Formal Logic It's a problem set, they

    It's a problem set, they are attached. it's related to Sider's book which is "Logic to philosophy" I attached the book too. I need it on feb22 but feb23 still work

    		•
  • Q : Explain trading of call options Explain

    Explain trading of call options.

    		•
  • Q : Problem on Nash equilibrium In a

    In a project, employee and boss are working altogether. The employee can be sincere or insincere, and the Boss can either reward or penalize. The employee gets no benefit for being sincere but gets utility for being insincere (30), for getting rewarded (10) and for be

    		•
  • Q : Solve each equation by factoring A

    A college student invested part of a $25,000 inheritance at 7% interest and the rest at 6%.  If his annual interest is $1,670 how much did he invest at 6%?  If I told you the answer is $8,000, in your own words, using complete sentences, explain how you

    		•
  • Q : Elementary Logic Set & Model of a

    Prove that Elementary Logic Set is a Model of a Boolean Algebra The three Boolean operations of Logic are the three logical operations of  OR ( V ), AN

    		•
  • Q : Calculus I need it within 4 hours. Due

    I need it within 4 hours. Due time March 15, 2014. 3PM Pacific Time. (Los Angeles, CA)

    		•