--%>
Assignment Help - homework help

Define Well-formed formulas or Wffs

Wffs (Well-formed formulas): These are defined inductively by the following clauses:
  
(i) If  P  is an n-ary predicate and  t1, …, tn are terms, then P(t1, …, tn) is a wff. (Such a wff is atomic.)

(ii)  If α is wff, then ¬ α is a wff.
  
(iii)  If α and β are wffs, then α → β is a wff.  
 
(iv) If α is a wff and x is an individual variable then

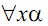
1946_v.jpg

is a wff. 
 
The connectives are operators, which act on wffs, yielding other wffs; ¬ is a unary operator (it acts on a single wff), → is a binary operator. Also a quantifier, coupled with a variable, is a unary operator that acts on wffs. We require that any wff that is thus generated has a unique decomposition into components. The notation should be such as to yield a unique readability theorem.

   Related Questions in Mathematics

  • Q : Who had find Monte Carlo and finite

    Who had find Monte Carlo and finite differences of the binomial model?

    		•
  • Q : Problem on sales and budget XYZ Farm

    XYZ Farm Supply data regarding the store's operations follow: • Sales are budgeted at $480,000 for November, $430,000 for December, and $340,000 for January. • Collections are expected

    		•
  • Q : Explain Factorisation by Fermats method

    Factorisation by Fermat's method: This method, dating from 1643, depends on a simple and standard algebraic identity. Fermat's observation is that if we wish to nd two factors of n, it is enough if we can express n as the di fference of two squares.

    		•
  • Q : Problem on Datalog for defining

    The focus is on  the use of Datalog for defining properties  and queries on graphs. (a) Assume that P is some property of graphs  definable in the Datalog. Show that P is preserved beneath extensions  and homomo

    		•
  • Q : Budgeted cash disbursements The ABC

    The ABC Company, a merchandising firm, has budgeted its action for December according to the following information: • Sales at $560,000, all for cash. • The invoice cost for goods purc

    		•
  • Q : Row-echelon matrix Determine into which

    Determine into which of the following 3 kinds (A), (B) and (C) the matrices (a) to (e) beneath can be categorized:       Type (A): The matrix is in both reduced row-echelon form and row-echelon form. Type (B): The matrix

    		•
  • Q : Mean and standard deviation of the data

    Below is the amount of rainfall (in cm) every month for the last 3 years in a particular location: 130 172 142 150 144 117 165 182 104 120 190 99 170 205 110 80 196 127 120 175

    		•
  • Q : State Measuring complexity Measuring

    Measuring complexity: Many algorithms have an integer n, or two integers m and n, as input - e.g., addition, multiplication, exponentiation, factorisation and primality testing. When we want to describe or analyse the `easiness' or `hardness' of the a

    		•
  • Q : Problem on inventory merchandise AB

    AB Department Store expects to generate the following sales figures for the next three months:                            

    		•
  • Q : Probability and Stochastic assignment

    Introduction to Probability and Stochastic Assignment 1: 1. Consider an experiment in which one of three boxes containing microchips is chosen at random and a microchip is randomly selected from the box.

    		•